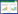服务
文章信息
- 李连伟, 鲁洪中, 夏建业, 储炬, 庄英萍, 张嗣良
- Li Lianwei, Lu Hongzhong, Xia Jianye, Chu Ju, Zhuang Yingping, Zhang Siliang
- 黑曲霉产糖化酶黑箱模型的构建和应用
- Construction and application of black-box model for glucoamylase production by Aspergillus niger
- 生物工程学报, 2015, 31(7): 1089-1098
- Chin J Biotech, 2015, 31(7): 1089-1098
- 10.13345/j.cjb.140634
-
文章历史
- Received: December 24, 2014
- Accepted: March 17, 2015
糖化酶是一种由微生物分泌的具有外切酶活性的胞外酶。作为一种酸性蛋白酶,主要功能是从多聚糖 (例如淀粉) 的非还原性末端水解释放β-D-葡萄糖[1]。糖化酶主要应用于食品、制药、发酵等工业[2]。黑曲霉由于高效的蛋白分泌能力广泛应用于糖化酶的工业生产,产量达20 g/L以上[3, 4]。为进一步提高糖化酶产量,发酵过程的优化和设计对于提高糖化酶的生产是十分必要的。
对于微生物产酶发酵过程首先是要了解菌体生长与产酶之间的关系,关于黑曲霉生长与产酶之间的相关性的研究已有大量报道。Schrickx等[5]研究了不同黑曲霉菌株在以葡萄糖和麦芽糊精为底物时菌体生长与产酶的关系,发现糖化酶生产与菌体生长相关,而且在以麦芽糊精为底物时,当菌体比生长速率大于0.15 h-1,比产物形成速率不再随比生长速率的增加而增加。Metwally等[6]的研究也表明以麦芽糖为底物、比生长速率在0.046-0.2 h-1范围内时,糖化酶的生成与菌体生长相关;而Pedersen等[7]的研究 结果表明在高比生长速率条件下,产酶与菌体生长不相关。
相对于单纯的发酵过程优化,构建数学模型更有利于深化对黑曲霉产糖化酶发酵过程的认识[8]。关于丝状菌产酶的数学模型已有大量的报道。Wang的模型描述了重组黑曲霉生产蛋白酶的发酵过程[9]。Albaek等[10]成功地模拟了不同通气和搅拌下米曲霉发酵过程中菌体的生长、底物的消耗和酶的生成。Ma等[11]构建了里氏木霉生产纤维素酶的模型并用于设计补料策略使酶产率增加了82.31%。根据我们了解,到目前还没有关于黑曲霉生产糖化酶非结构模型的报道。
本文通过碳限制恒化实验研究了不同比生长速率下黑曲霉生长与糖化酶形成的关系。构建了黑曲霉产糖化酶发酵的黑箱模型,黑箱模型表明糖化酶的比形成速率与黑曲霉的比生长速率满足Luedeking-Piret方程。我们使用黑箱模型设计补料分批实验,使糖化酶的得率最高,并成功地使用模型描述了黑曲霉产糖化酶的发酵过程。
1 模型 1.1 反应方程黑曲霉产糖化酶的发酵过程可以用下面的反应式 (1) 来描述[12]。式中,${{Y}_{SN}}$、${{Y}_{SO}}$、${{Y}_{SX}}$、${{Y}_{SP}}$、${{Y}_{SC}}$和${{Y}_{SH}}$表示基于底物的氮源、氧气、菌体、产物、二氧化碳和水的表观得率系数,部分表观得率系数可以通过恒化实验的比速率计算得到 (方程2);${{q}_{I}}$、${{q}_{S}}$表示比速率和比底物消耗速率;${{Y}_{SI}}$表示基于底物的表观得率系数。反应式 (1) 可以计算碳限制恒化实验下的碳平衡和还原力平衡用来检验所得实验数据的可靠性。
| \[\begin{align} &C{{H}_{2}}O(\text{substrate})+{{Y}_{SN}}N{{H}_{3}}+{{Y}_{SO}}{{O}_{2}}\to \\ &{{Y}_{SX}}C{{H}_{1.72}}{{O}_{0.55}}{{N}_{0.17}}(\text{biomass})+{{Y}_{SP}}C{{H}_{1.52}}{{O}_{0.34}}{{N}_{0.25}} \\ &(product)+{{Y}_{SC}}C{{O}_{2}}+{{Y}_{SH}}{{H}_{2}}O \\ \end{align}\] | (1) |
| \[{{Y}_{SI}}=\frac{{{q}_{I}}}{{{q}_{S}}}\] | (2) |
比底物消耗速率与底物浓度的关系可以用Monod动力学模型表征 (方程式3),${{q}_{S,\max }}$是黑曲霉最大底物消耗速率,${{k}_{S}}$是碳限制生长条件下底物的饱和常数。
| \[{{q}_{S}}=\frac{{{q}_{S,\max }}{{C}_{S}}}{{{K}_{S}}+{{C}_{S}}}\] | (3) |
菌体生长与产酶之间的关系可以用Luedeking- Piret模型来表示[13]。根据Luedeking-Piret模型可以将菌体生长与酶的生产分为生长相关型、部分生长相关型、生长不相关。根据黑曲霉产糖化酶的相关研究发现在一定比生长速率范围内产酶是生长相关的,而在高比生长速率下与生长不再相关。因此,在本文的研究中也使用Luedeking-Piret模型 (方程4) 来描述菌体生长与产酶的关系。
| \[{{q}_{p}}=a\mu +b\] | (4) |
比底物消耗速率和比氧消耗速率使用Herbert-Pirt方程来描述 (方程5和6)[14]。其中$Y_{SX}^{\max }$、$Y_{SP}^{\max }$是基于底物的最大菌体和最大产物得率,$m_{S}^{{}}$用于维持菌体的底物消耗。$Y_{OX}^{\max }$、$Y_{OP}^{\max }$是基于氧的最大菌体和最大产物得率,${{m}_{{{O}_{2}}}}$用于维持菌体的氧消耗。
| \[{{q}_{S}}=\frac{\mu }{Y_{SX}^{\max }}+\frac{{{q}_{p}}}{Y_{SP}^{\max }}+{{m}_{S}}\] | (5) |
| \[{{q}_{{{O}_{2}}}}=\frac{\mu }{Y_{OX}^{\max }}+\frac{{{q}_{p}}}{Y_{OP}^{\max }}+{{m}_{{{O}_{2}}}}\] | (6) |
使用黑箱模型设计补料分批实验,结合数学模型验证获得黑箱模型的准确性。发酵过程中发酵液质量M (单位kg)、生物量X (单位g)、底物量S (单位g)、产物量P (单位g) 的变化可以使用方程7-10描述[10]。
| \[\frac{dM}{dt}={{F}_{in}}-{{F}_{evap}}\] | (7) |
| \[\frac{dX}{dt}=\mu X\] | (8) |
| \[\frac{dS}{dt}={{F}_{in}}{{C}_{S,in}}-{{q}_{S}}X\] | (9) |
| \[\frac{dP}{dt}={{q}_{p}}X\] | (10) |
式中,${{F}_{in}}$表示补料补加速率 (单位kg/h),${{F}_{evap}}$表示发酵液蒸发损失 (单位kg/h),$\mu$表示菌体比生长速率 (单位/h),${{C}_{S,in}}$表示补料中糖浓度 (单位g/kg),${{q}_{S}}$表示比底物消耗速率 (单位g/(g DCW·h)),${{q}_{P}}$表示比产物形成速率 (单位g/(g DCW·h))。
1.4 模型的求解和模拟使用OriginPro 9.0软件拟合恒化培养实验数据获得黑箱模型参数。补料分批培养模拟使用MATLAB,version 2009b,微分方程求解使用ode45求解器。
2 材料与方法 2.1 菌株和培养基黑曲霉菌株GAM15由荷兰皇家帝斯曼集团 (DSM) 提供,是一株糖化酶生产的突变株。
种子培养基包含:22 g/L一水葡萄糖和20 g/L固体玉米浆。分批培养使用合成培养基包含:10 g/L一水葡萄糖,3 g/L (NH4)2SO4,3 g/L KH2PO4,0.02 g/L ZnCl2,1.69 g/L KH2PO4·2H2O,0.67 g/L EDTA,1.0 g/L MgSO4·7H2O,0.076 g/L CaCl2,0.015 g/L CuSO4·5H2O,0.015 g/L CoCl2·6H2O,0.04 g/L MnSO4·4H2O,0.3 g/L FeSO4·7H2O和 1 mL/L消泡剂。恒化培养的培养基与分批培养培养基基本一致,只是一水葡萄糖变为9.35 g/L,(NH4)2SO4变为2.5 g/L。培养基采用高温灭菌,葡萄糖单独灭菌并在无菌条件下加入到培养基中。
指数补料分批培养过程中,分批培养使用合成培养基包含:13.2 g/L一水葡萄糖,3 g/L (NH4)2SO4,3 g/L KH2PO4,0.02 g/L ZnCl2,1.69 g/L KH2PO4·2H2O,0.67 g/L EDTA,1.0 g/L MgSO4·7H2O,0.076 g/L CaCl2,0.015 g/L CuSO4·5H2O,0.015 g/L CoCl2·6H2O,0.04 g/L MnSO4·4H2O,0.3 g/L FeSO4·7H2O 和1 mL/L 消泡剂。补料培养基与分批培养培养基基本一致,只是一水葡萄糖变为220 g/L。培养基采用高温灭菌,葡萄糖单独灭菌并在无菌条件下加入到培养基中。
2.2 培养条件种子培养使用带挡板的摇瓶,包含100 mL种子培养基,107孢子/mL孢子悬液接种1 mL,起始培养基pH维持在6.5,摇床转速150 r/min,种子培养24 h。
碳限制恒化实验使用5 L发酵罐 (上海国强生化工程装备公司),通过控制恒定液面方法控制发酵液体积控制在3 L,使用3 mol/L NaOH控制pH 4.5,通气量3 L/min,搅拌转速375 r/min (2平叶桨),温度控制 (34±0.1) ℃。当分批培养葡萄糖耗尽和溶氧上升时,由分批培养转为恒化培养。当发酵液完成5个洗脱体积,二氧化碳生成速 率、酶浓度、菌浓保持恒定时恒化培养达到稳态。
指数补料分批实验使用5 L发酵罐 (上海国强生化工程装备公司),初始发酵液体积为3 L,使用氨水控制pH 4.5,通气量3 L/min,搅拌转速375‒525 r/min (2平叶桨),温度控制 (34±0.1) ℃。
2.3 分析方法 2.3.1 酶活测定酶活使用淀粉葡萄糖苷酶 (AGI) 表示。一个AGI单位定义为在pH 4.3和温度60 ℃条件下每分钟从可溶性淀粉水解生成1 µmol葡萄糖所需的酶量。50 mg糖化酶标品对应大约2 500 AGI。糖化酶酶活测量:230 µL p-硝基苯基-α-D-吡喃葡萄糖苷 (AGIsub) 试剂 (37 ℃预热5 min) 与20 µL发酵液上清混合,37 ℃反应20 min后加100 µL AGIstop试剂,在405 nm下测量混合液体吸光度来定量糖化酶。
2.3.2 菌浓测定采用抽滤方法使用孔径0.8 µm的玻璃纤维滤膜过滤菌体,使用50 mL去离子水洗涤菌体,70 ℃干燥24 h称量滤膜重量。
2.3.3 葡萄糖测定恒化稳态下葡萄糖浓度测定使用Dionex ICS 3000 (Dionex,Sunnyvale,CA) 离子色谱。分离柱Carbopac PA 200,柱温30 ℃,流动相3 mmol/L NaOH,流速0.35 mL/min,检测器电化学检测器 (ED40)。
2.3.4 尾气测定发酵过程中,氧气的消耗速率和二氧化碳的生成速率使用过程质谱仪 (MAX300-LG,Extrel) 测定。溶氧使用极谱溶氧电极 (Mettler Toledo) 测定。
3 结果与分析 3.1 恒化实验结果 3.1.1 Monod 动力学模型在葡萄糖限制恒化、不同稀释率培养条件下,稳态下的葡萄糖浓度${{C}_{Glc}}$与比葡萄糖消耗速率${{q}_{Glc}}$的关系满足Monod方程的形式 (图1)。其中最大葡萄糖消耗速率${{q}_{Glc,\max }}$=0.34 g/(g DCW·h) 是根据分批培养指数生长阶段最大比生长速率和恒化实验得到的Herbert-Pirt方程计算得到的。葡萄糖的饱和常数${{K}_{Glc}}$=6.4 mg/L是通过Monod方程拟合得到的。这与Carlsen等[15]在米曲霉产α-淀粉酶恒化培养中得到的葡萄糖饱和常数是十分接近的。

|
| 图1 黑曲霉葡萄糖限制恒化培养下比生长速率与葡萄糖浓度的关系 Fig.1 Relation of specific glucose consumption rate and the concentration of glucose at glucose-limited continuous culture by Aspergillus niger. |
在葡萄糖限制恒化培养稳态条件下,糖化酶的浓度随比生长速率的增加而增加,并在µ=0.08 h-1时达到最大 (图2A)。糖化酶浓度随比生长速率的变化趋势与Metwally的实验结果相似[16]。另外,实验中也发现在比生长速率低于0.03 h-1时连续培养超过2个洗脱体积会出现发酵液的褐化现象,菌体的形态发生改变而且稳态后的糖化酶浓度是褐化前的两倍 (图2A中的空心实验点数据),可能与菌体的突变和退化有关[17]。

|
| 图2 黑曲霉葡萄糖限制恒化培养下糖化酶浓度(A)、比糖化酶形成速率(B)与比生长速率的关系 Fig.2 Relation of concentration of glucoamylase (A),the specific glucoamylase formation rate (B) and the specific growth rate at glucose-limited continuous culture by Aspergillus niger. |
研究葡萄糖限制恒化培养条件下比产物形成速率与比生长速率的关系发现,在0‒0.068 h-1范围内比产物形成速率与比生长速率呈线性关系,糖化酶的形成与菌体的生长是相关的 (图2B)。当比生长速率大于0.068 h-1时,比产物形成速率不再随比生长速率的增加而增加,糖化酶的形成不依赖于菌体生长,而且在高比生长速率下糖化酶的形成受到抑制。在相关黑曲霉产糖化酶的研究中,Metwally等[5, 6]在以麦芽糖为底物恒化培养条件下和Schrickx等[5, 6]以葡萄糖为底物恒化培养条件下,发现比生长速率0.04‒0.2 h-1范围内比糖化酶的形成速率与比生长速率是相关的,而Schrickx等[5, 6]以麦芽糊精为底物恒化培养条件下也发现当比生长速率大于0.15 h-1时,糖化酶形成与菌体的生长不相关。Pedersen等[7]在研究以葡萄糖和麦芽糖为底物的批培养、恒化培养和补料分批培养过程中发现,在比生长速率0‒0.1 h-1范围内比糖化酶形成速率线性增加,而在0.1‒0.2 h-1范围内比糖化酶形成速率恒定。分析造成高比生长速率条件下比糖化酶形成速率不再增加的原因,可能是出现葡萄糖分解代谢物阻遏作用和在高比生长速率下更多能量用于菌体生长。
3.1.3 底物消耗 Herbert-Pirt 方程如图3所示,葡萄糖限制恒化培养条件下,比葡萄糖消耗速率、菌体比生长速率和比糖化酶形成速率满足Herbert-Pirt方程的形式,非线性曲面拟合的结果显示三者之间有很好的相关性。通过拟合底物利用的Herbert-Pirt方程得到生长相关的参数。基于葡萄糖的最大菌体得率,$Y_{SX}^{\max }$,本文研究的黑曲霉菌株0.62 g菌体/g葡萄糖与Metwally报道的0.64 g菌体/g葡萄糖十分接近,比Schrickx研究结果0.56 g菌体/g葡萄糖略高。菌体的维持系数mS与Metwally结果十分接近[5, 6]。而基于葡萄糖的最大糖化酶得率,$Y_{SP}^{\max }$=0.79 g糖化酶/g葡萄糖,在相关文献中并没有报道 (表1)。

|
| 图3 黑曲霉葡萄糖限制恒化培养下比葡萄糖消耗速率与比生长速率、比产物形成速率的关系 Fig.3 Relation of the specific glucose consumption rate,the specific growth rate and the specific glucoamylase formation rate under glucose-limited continuous culture by Aspergillus niger. |
| Parameter | Unit | our study | Metwally et al[6] | Schrickx et al[5] |
| ${{q}_{Glc,\max }}$ | g/(g DCW·h) | 0.34 | _ | _ |
| ${{K}_{Glc}}$ | mg/L | 6.4 | _ | _ |
| $Y_{SX}^{\max }$ | g/g | 0.62 | 0.64 | 0.56 |
| $Y_{SP}^{\max }$ | g/g | 0.79 | _ | _ |
| mS | g/(g DCW·h) | 0.04 | 0.04 | 0.01 |
| $Y_{OX}^{\max }$ | g/g | 3.28 | 3.10 | 1.71 |
| $Y_{OP}^{\max }$ | g/g | 1.56 | _ | _ |
| MO2 | g/(g DCW·h) | 0.05 | 0.05 | 0.01 |
| a | g/g | 0.41 | _ | _ |
| b | g/(g DCW·h) | 0.0267 | _ | _ |
如图4所示,葡萄糖限制恒化培养条件下,比氧消耗速率、菌体比生长速率和比糖化酶形成速率满足Herbert-Pirt方程的形式,非线性曲面拟合的结果显示三者之间有很好的相关性。通过拟合氧利用的Herbert-Pirt方程得到生长相关的参数。基于氧的最大菌体得率$Y_{OX}^{\max }$,本文研究的黑曲霉菌株3.28 g菌体/g O2比Metwally报道的3.13 g菌体/g O2略高,而远大于Schrickx研究菌株1.71 g菌体/g O2[5]。菌体的维持系数${{m}_{O2}}$与Metwally结果十分接近[6]。从获得的参数可以看出本文研究黑曲霉菌株的氧利用效率更高。而基于氧的最大糖化酶得率,$Y_{OP}^{\max }$=1.56 g糖化酶/g O2,相比于菌体基于氧的得率,糖化酶的形成对能量的需求更高 (表1)。
|
| 图4 黑曲霉葡萄糖限制恒化培养下比氧消耗速率与比生长速率、比产物形成速率的关系 Fig.4 Relation of the specific oxygen consumption rate,the specific growth rate and the specific glucoamylase formation rate under glucose-limited continuous culture by Aspergillus niger. |
葡萄糖限制恒化实验获得的黑箱模型包括葡萄糖消耗Monod方程,葡萄糖和氧消耗的Herbert-Pirt方程,以及描述酶生成与菌体生长相关性的Luedeking-Piret方程,黑箱模型中所有比速率都可以表征为比生长速率μ的函数${{q}_{i}}(\mu )$。为验证获得的黑箱模型的准确性,根据黑箱模型设计补料策略实现糖化酶相对葡萄糖消耗的得率最大,在补料分批发酵过程中控制菌体的比生长速率在0.05 h-1。
要控制补料分批发酵过程中菌体比生长速率恒定,补料过程中葡萄糖的补料曲线可以用方程 (11) 来表示。
| \[{{F}_{S}}(t)=\left| {{q}_{Glc,opt}} \right|{{N}_{X}}({{t}_{f}})exp({{\mu }_{opt}}(t-{{t}_{f}}))\] | (11) |
式中,${{F}_{S}}(t)$表示葡萄糖补加速率 (单位g/h),${{q}_{Glc,opt}}$表示最适比生长速率下的比底物消耗速率 (单位g/(g DCW·h)),NX(tf) 表示分批培养结束时菌量 (单位g),${{\mu }_{opt}}$表示最适比生长速率 (单位/h),tf表示分批培养结束时间 (单位h)。
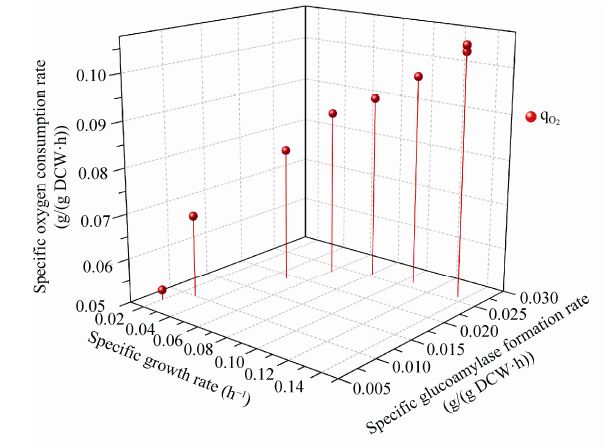
3.2.2 指数补料分批发酵实验结果碳限制条件下指数补料分批发酵过程如图5所示,整个发酵过程溶氧水平在20%以上,并未出现氧限制。在分批培养发酵结束溶氧开始上升时开始指数补料,指数补料发酵时间持续29 h。
|
| 图5 指数补料分批培养下葡萄糖 (A)、生物量(B)、糖化酶(C)和OUR (D)实验值与模拟值比较 Fig.5 Comparison between the experimental data and the model predicted results of glucose (A),biomass (B),glucoamylase (C) and OUR (D) under exponential fed-batch culture. |
实验值与模拟值比较见图5,从图5中可以看出黑箱模型可以很好地预测指数补料分批发酵过程中葡萄糖的消耗、菌体的形成、糖化酶的形成和氧的消耗。模型预测值和实验值相对误差都在10%以内,糖量模型预测值与实验值相对误差平均为4.3%;菌量模型预测值与实验值相对误差平均为9.5%;糖化酶量模型预测值与实验值相对误差平均为9.7%;OUR模型预测值与实验值相对误差平均为5.9%;菌量模拟预测值与实验值相对误差较大,分析主要原因是由于发酵过程后期生物量较高,黑曲霉出现挂壁现象,导致在发酵后期菌体实验值略低于模拟值。
通过计算发酵过程中相关得率数据,发现糖化酶基于菌体的得率实验值0.407 (g糖化酶/g菌体) 与模拟值得率0.403 (g糖化酶/g菌体) 十分接近,而且糖化酶基于葡萄糖的得率实验值0.127 (g糖化酶/g葡萄糖) 与模拟值最大得率0.134 (g糖化酶/g葡萄糖) 的相对误差为5.5%。从指数补料分批发酵的实验结果可以看出,恒化实验获得的黑箱模型可以用于设计黑曲霉产糖化酶的发酵过程。根据黑箱模型模拟结果,在较低的比生长速率下葡萄糖更多地用于维持菌体代谢,而在高比生长速率下,菌体的生长与糖化酶的形成存在竞争关系,葡萄糖优先用于菌体的生长而抑制了糖化酶的形成,通过控制菌体在最适比生长速率使更多葡萄糖用于糖化酶的形成,可以实现糖化酶的得率最高。
4 结论基于葡萄糖限制下恒化实验黑曲霉生长与糖化酶生产相关性的研究发现,在比生长速率低于0.068 h-1时糖化酶生产与菌体生长相关,而比生长速率高于0.068 h-1时糖化酶生产与菌体生长不相关。采用底物消耗Monod方程、Herbert-Pirt方程和Luedeking-Piret方程构建的黑曲霉产糖化酶的黑箱模型能够很好地描述发酵过程中底物消耗、菌体的生长、产物的形成。
相比于碳限制发酵实验,氧限制更有利于黑曲霉产糖化酶发酵过程[18, 19, 20]。而基于碳限制的数学模型在黑曲霉产糖化酶补料分批发酵过程的成功应用,对于氧限制条件下黑曲霉产糖化酶发酵过程的设计和优化具有借鉴意义,并可以为发酵过程的进一步放大提供指导。
| [1] | Marín-Navarro J, Polaina J. Glucoamylases: structural and biotechnological aspects. Appl Microbiol Biotechnol, 2011, 89(5): 1267-1273. |
| [2] | Kumar P, Satyanarayana T. Microbial glucoamylases: characteristics and applications. Crit Rev Biotechnol, 2009, 29(3): 225-255. |
| [3] | van Brunt J. Fungi: the perfect hosts? Nat Biotechnol, 1986, 4(12): 1057-1062. |
| [4] | Grimm LH, Kelly S, Krull R, et al. Morphology and productivity of filamentous fungi. Appl Microbiol Biotechnol, 2005, 69(4): 375-384. |
| [5] | Schrickx JM, Krave AS, Verdoes JC, et al. Growth and product formation in chemostat and recycling cultures by Aspergillus niger N402 and a glucoamylase overproducing transformant, provided with multiple copies of the glaA gene. J Gen Microbiol, 1993, 139(11): 2801-2810. |
| [6] | Metwally M, el Sayed M, Osman M, et al. Bioenergetic consequences of glucoamylase production in carbon-limited chemostat cultures of Aspergillus niger. Antonie Van Leeuwenhoek 1991, 59(1): 35-43. |
| [7] | Pedersen H, Beyer M, Nielsen J. Glucoamylase production in batch, chemostat and fed-batch cultivations by an industrial strain of Aspergillus niger. Appl Microbiol Biotechnol, 2000, 53(3): 272-277. |
| [8] | Thilakavathi M, Basak T, Panda T. Modeling of enzyme production kinetics. Appl Microbiol Biotechnol, 2006, 73(5): 991-1007. |
| [9] | Wang L, Ridgway D, Gu T, et al. Kinetic modeling of cell growth and product formation in submerged culture of recombinant Aspergillus niger. Chem Eng Commun, 2008, 196(4): 481-490. |
| [10] | Albaek MO, Gernaey KV, Hansen MS, et al. Modeling enzyme production with Aspergillus oryzae in pilot scale vessels with different agitation, aeration, and agitator types. Biotechnol Bioeng, 2011, 108(8): 1828-1840. |
| [11] | Ma L, Li C, Yang Z, et al. Kinetic studies on batch cultivation of Trichoderma reesei and application to enhance cellulase production by fed-batch fermentation. J Biotechnol, 2013, 166(4): 192-197. |
| [12] | Nielsen J. Modelling the growth of filamentous fungi, in modern biochemical engineering. Adv Biochem Eng/Biotechnol, 1992, 46: 189-201. |
| [13] | Luedeking R, Piret EL. A kinetic study of the lactic acid fermentation. batch process at controlled pH. Biotechnol Bioeng, 2000, 67(6): 636-644. |
| [14] | Van Gulik W, Antoniewicz M, DeLaat W, et al. Energetics of growth and penicillin production in a high-producing strain of Penicillium chrysogenum. Biotechnol Bioeng, 2001, 72(2): 185-193. |
| [15] | Carlsen M, Nielsen J, Villadsen J. Growth and α-amylase production by Aspergillus oryzae during continuous cultivations. J Biotechnol, 1996, 45(1): 81-93. |
| [16] | Metwally M. Glucoamylase production in continuous cultures of Aspergillus niger with special emphasis on growth parameters. World J Microbiol Biotechnol, 1997, 14(1): 113-118. |
| [17] | Withers JM, Swift RJ, Wiebe MG, et al. Optimization and stability of glucoamylase production by recombinant strains of Aspergillus niger in chemostat culture. Biotechnol Bioeng, 1998, 59(4): 407-418. |
| [18] | Pedersen L, Hansen K, Nielsen J, et al. Industrial glucoamylase fed-batch benefits from oxygen limitation and high osmolarity. Biotechnol Bioeng, 2012, 109(1): 116-124. |
| [19] | Diano A, Peeters J, Dynesen J, et al. Physiology of Aspergillus niger in oxygen-limited continuous cultures: influence of aeration, carbon source concentration and dilution rate. Biotechnol Bioeng, 2009, 103(5): 956-965. |
| [20] | Diano A, Bekker-Jensen S, Dynesen J, et al. Polyol synthesis in Aspergillus niger: influence of oxygen availability, carbon and nitrogen sources on the metabolism. Biotechnol Bioeng, 2006, 94(5): 899-908. |
 2015, Vol. 31
2015, Vol. 31