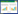文章信息
- 徐开琨, 韩明飞, 黄传玺, 常乘, 朱云平
- Xu Kaikun, Han Mingfei, Huang Chuanxi, Chang Cheng, Zhu Yunping
- 基于质谱的蛋白质生物标志物发现中的特征选择与机器学习方法研究进展
- Research progress of feature selection and machine learning methods for mass spectrometry-based protein biomarker discovery
- 生物工程学报, 2019, 35(9): 1619-1632
- Chinese Journal of Biotechnology, 2019, 35(9): 1619-1632
-
文章历史
- Received: February 14, 2019
- Accepted: May 5, 2019
- Published: May 13, 2019
2. 国家蛋白质科学中心 (北京) 北京蛋白质组研究中心 蛋白质组学国家重点实验室,北京 102206;
3. 河北大学 生命科学学院,河北 保定 071002
2. State Key Laboratory of Proteomics, Beijing Proteome Research Center, National Center for Protein Sciences (Beijing), Beijing 102206, China;
3. College of Life Sciences, Hebei University, Baoding 071002, Hebei, China
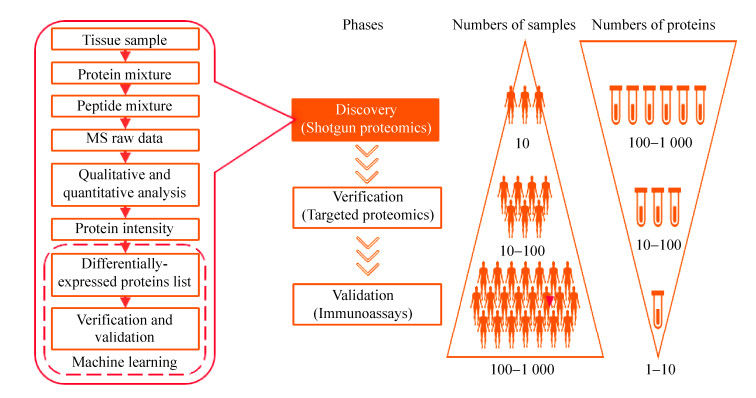
生物标志物(Biomarker)是指“一种可客观检测和评价的指标,可作为正常生物学过程、病理过程或治疗干预药理学反应的指示因子”[1],对于筛查、诊断或监测疾病,指导分子靶向治疗以及评估治疗效果等具有重要的意义[2-4]。作为中心法则末端承担生命活动的载体,由于存在可变剪切、单核苷酸多态性及翻译后修饰,蛋白质的状态包含更多维度的信息,与生命活动的各个方面息息相关,更加适合作为生物标志物[5]。目前美国国家癌症研究所(National cancer institute)发布的EDRN数据库(Early detection research network, https://edrn.nci.nih.gov)针对十种器官共收录了583种蛋白质生物标志物,占收录的全部生物标志物的57%。此外,几乎所有被FDA批准应用于临床的标志物如甲胎蛋白(Alpha-fetoprotein, AFP)等都是蛋白质。与此同时,质谱技术凭借其高通量、高灵敏性等优点已经成为了蛋白质组研究的主流技术[6]。将质谱方法用于蛋白质生物标志物发现已成为蛋白质组的研究热点之一,近年来相关文献数目增长迅速(图 1)。
|
| 图 1 PubMed数据库中蛋白质生物标志物相关文献数目统计 Fig. 1 Number of related literatures contains both "proteomics" and "biomarker" on PubMed database. |
| |
目前蛋白质生物标志物的发现多基于实验组与对照组之间的蛋白质丰度差异,呈现出两种策略:经典的生物标志物发现策略可分为蛋白质生物标志物发现、确认和验证三个阶段,由于其各阶段所需的样本数目及候选蛋白质数目按照数量级变化(图 2),之后的研究中常称其为“三角”发现策略;另一种策略类似于全基因组关联分析(Genome-wide association study,GWAS),通过进行大队列非靶向的蛋白质组数据分析,发现蛋白质表达量、修饰状态的改变和疾病状态的相关性[7-10],又被称为“矩形”发现策略[11]。两种策略中研究人员均通过鸟枪法蛋白质组定量结果进行分析,寻找在实验组与对照组之间的差异表达蛋白质,继而确定可能的蛋白质生物标志物。如何从高维蛋白质组数据中寻找出能更具区分能力的标志物,如何评价所选的生物标志物的分类效果是方法学研究中最为关注的两个问题。前者可以抽象为特征选择;后者则可等效为分类器的效能评估[12]。
在传统的差异表达蛋白质筛选方法中,研究人员根据实验设计类型以及数据的正态性与方差齐性,选择采用参数检验(如t检验、u检验、方差分析ANOVA等)或非参数检验(如Mann-Whitney U检验、Wilcoxon秩和检验、Kruskal-Wallis H检验等)判断样本均数是否具有统计学差异,而后采用多元线性回归、逻辑回归等回归模型评判蛋白质生物标志物的分类效果。这些方法存在以下问题:1)尽管假设检验方法具有丰富的理论支持及应用实例,但其本质上都是单变量的分析手段。由于协同或者拮抗作用的存在,同一条通路上的蛋白质常呈现出相同或相反的变化趋势,传统的分析方法不能反映蛋白质之间的相关性。2)生物标志物能够被用于区分疾病和正常组,在数学上可以看成一个分类问题。传统的回归模型更适用于处理单一边界线性可分的分类问题,而以蛋白质组数据为例的组学数据往往是非线性可分的,只应用线性回归模型可能导致分类效果不佳。3)很难通过图像表示出高维空间中的线性超平面,传统回归分析缺乏直观的可视化手段。
这些问题来源于蛋白质组数据的“高维度”与“稀疏性”,需要通过对数据进行简化来解决。特征选择与机器学习方法在其中有广泛的应用。依据训练数据是否拥有标记信息,机器学习方法可分为“无监督学习方法”与“监督学习方法”两类。本文将详细描述蛋白质生物标志物发现中特征选择方法及这两类机器学习方法的具体应用。
1 特征选择方法特征选择(Feature selection, FS)被定义为“从给定的特征集合中选择出相关特征集的过程[14]”,可以看作是机器学习方法的“预处理”阶段,目的是选择重要的特征并去除不相关的特征。特征选择的通用做法是首先生成一个特征子集并评价其好坏,依据评价结果产生下一个特征子集,如此循环迭代至找不到更好的特征子集为止,这一过程涉及到子集搜索(Subset search)与子集评价(Subset evaluation)两个环节。
在特征选择之前需要对数据进行缺失值插补及标准化等操作,已有一些综述对其进行了总结[15-16],此处不作展开叙述。
常见的特征选择方法分为过滤式(Filters)、包裹式(Wrappers)及嵌入式(Embedded methods)三种类型。
1.1 过滤式选择过滤式方法首先对数据集进行特征选择,而后训练机器学习模型,特征选择的过程与后续的模型无关。过滤式方法需要构建用以衡量特征的重要性的统计量。
单变量的过滤方法(信息增益[17]、Relief[18]、统计学t检验等)仅对单个特征进行评估,此类选择方法往往计算成本较低且具有较强的鲁棒性,但是容易保留冗余特征。
为了解决此类问题,多变量的过滤方法(最小冗余最大相关mRMR[19]等)会分析整个特征子集,基于相关性减少冗余特征。Shen等[20]在研究中使用mRMR方法对胰腺癌转录组数据进行特征选择。
1.2 包裹式选择包裹式方法直接把机器学习模型的性能作为子集的评价准则,为分析模型选择最有利于其性能的特征子集。这类选择方法往往考虑了特征间的相关性,在每次迭代中生成并测试多个特征子集,较为典型的过滤式方法是LVM (Las vegas wrapper)。
此类方法的效能往往要好于过滤式方法,但是在样本数量有限的条件下容易出现过拟合,且有显著的计算成本提升。
1.3 嵌入式选择在前两种方法中,特征选择过程与机器学习模型有着明显的区分,嵌入式选择将二者融为一体,将特征选择集成到分类模型的构造中,主要目的是为了结合过滤式与包裹式方法的优点。决策树(Decision tree,DT)与随机森林(Random forest,RF)、支持向量机(Support vector machine,SVM)等监督学习算法都属于此类,算法与应用将在本文第四节详细介绍,这些算法在使用时首先过滤式地对特征空间进行降维,而后采用包裹式方法选取最佳的特征子集。
2 无监督学习方法无监督学习方法的目的在于发现隐藏的数据结构或变量之间的关联。在这种情况下,训练数据不需要任何手工标注的标签,其中的代表方法包括主成分分析(Principal component analysis,PCA)及层次聚类(Hierarchical clustering)。
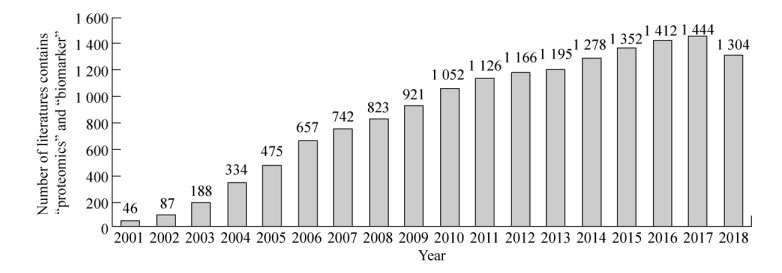
2.1 主成分分析PCA是蛋白质组学中使用较早的机器学习方法,其核心思想是通过对协方差矩阵进行特征分解,以得出数据的主成分与它们的权值。经过这种操作可以将原始数据的n维特征映射到k (k<n)维上形成全新的正交特征,即主成分(Principal components,PCs),是将原始的特征线性组合所重新构造出来的新特征,而非简单地从n维特征中去除其余n−k维特征。PCA中评估结果好坏有两个主要指标:成分载荷(Component loadings)指主成分与原始特征之间的关联系数,成分得分(Component scores)指样本在各主成分维度上的值,这二者与输入矩阵之间满足如图 3A所示的关系。由于主成分是由原始特征加权求和计算而来,是一种破坏性的操作,很难将主成分的重要性排序反推到原始特征之上,导致单一使用PCA在原始特征贡献度注释方面并无优势。PCA结果的可视化通常使用散点图来表示(图 3B),其坐标轴对应于两个不同的主成分,且二者对总体方差的贡献并不要求最大。
|
| 图 3 蛋白质生物标志物发现中的无监督学习方法 Fig. 3 Unsupervised learning methods in the identification of protein biomarkers. (A) Dimensional relationship in principal component analysis. (B) Schematic diagram of principal component analysis output, proportion of variance of PC1 is 54.8% and of PC2 is 25.2%. (C) The heatmap of hierarchical clustering shows that the tree diagram on the horizontal axis can successfully separate the treatment group from the control group and the tree diagram on the vertical axis divides the protein into multiple categories according to the abundance change. Color in the heatmap indicates the intensity of the quantified proteins. |
| |
R语言有两种PCA的计算函数,prcomp和princomp,前者使用奇异值分解(Singular value decomposition,SVD)实现,后者采用实对称矩阵对角化方式实现。此外,Python语言的scikit-learn机器学习模块的decomposition类中也集成了PCA的相关功能。PCA的主要应用包括:1)对原始特征的异常值进行检验,如Blanchet等[21]对自身免疫性脑脊髓炎的研究工作。2)在相关主成分空间中为不同类别实现的分离结果的可视化,且由于成分载荷及成分得分提供了部分候选生物标志物的信息以及在实验条件中的上调或下调,故而在某些早期研究中使用PCA作为所选蛋白质生物标志物分类性能的评判标准,如Zhang等[22]在乳腺癌非侵袭性检测中筛选蛋白质生物标志物的工作。3)部分研究中将PCA用作评估生物标志物研究中测量重现性的工具,如Govorukhina等[23]关于宫颈癌血清样本的研究及Liggett等[24]分析SELDI-TOF对于蛋白质组测量重复性的研究。
2.2 层次聚类聚类分析试图通过“距离度量(Distance measure)”将数据集中的样本划分为若干个不相交的“簇”,每个簇对应于一些潜在的相似性概念。层次聚类是标志物筛选中使用频率较高的聚类方法,它试图在不同层次上对数据集进行划分从而最终形成树形的聚类结构。需要注意的是,聚类算法仅能自动形成簇结构,但簇对应的概念语义不存在通用的客观标准,往往需要使用者自行把握和命名。
在蛋白质组研究中,在蛋白质与样本两个维度同时进行层次聚类分析已经成为了一种通用的方法,可以同时获得样本聚类以及不同聚类中蛋白质丰度变化等信息。层次聚类的输出结果常常使用热图的方式给出(图 3C),热图颜色表示相关指标的高低,两轴上树状图距离越远的两个样本之间相似性越低。在树状图的不同层次上进行分割,可以得到不同的簇划分结果。R语言中hclust函数可用于绘制层次聚类的树状图,heatmap、heatmap.2及pheatmap函数可用于热图绘制。
在蛋白质生物标志物研究中层次聚类多一个可视化的评价手段,一方面可用作评估数据集的整体情况,Wit等[25]在发现结直肠癌生物标志物的工作中,对4例结直肠癌患者与4例正常对照患者的含2 703个分泌蛋白质的组学数据进行评估,分析显示形成3个簇,所有癌症患者形成1个簇,而正常对照分成2个簇,说明分泌蛋白质组在患者之中更为接近;层次聚类另一方面也用于评估方法参数性能,Griffin等[26]的工作中为了验证新的谱图定量方法SIN的特异性,对于10组分别来自肾脏和心脏分离的内皮细胞质膜进行蛋白质组分析,最后对SIN值进行无监督学习的双向层次聚类,发现可成功将两种样本完全分离。
2.3 无监督学习常用分析工具除了编程语言的功能函数外,还有许多分析工具或插件可以实现PCA及层次聚类的数据分析与图形绘制,我们在表 1中列出了常用分析工具及相关属性。
| Software | Client | Platform | Link |
| ClustVis[27] | Web | – | https://biit.cs.ut.ee/clustvis/ |
| Wessa.net | Web | – | https://www.wessa.net/ |
| BioVinci | Local | Windows/MacOS/Linux | https://vinci.bioturing.com/ |
| IBM SPSS statistics | Local | Windows/MacOS/Linux | https://www.ibm.com/analytics/spss-statistics-software |
| PLS toolbox | Local | Windows/MacOS/Linux (MATLAB) | http://www.eigenvector.com/software/pls_toolbox.htm |
| WEKA[28] | Local | Windows/MacOS/Linux | https://www.cs.waikato.ac.nz/ml/weka/ |
| XLSTAT | Local | Windows (Excel) | https://www.xlstat.com/en/ |
在监督学习方法中,系统必须首先“学习”一个用以描述数据的模型的目标函数,然后再将目标函数用于从一组输入变量中预测输出变量的值或所属分类。模型一般需要将输出变量与事先标记的人工标签(疾病分型、是否患病等)进行比对,通过最小化输出值与人工标签的差异提升模型的预测性能。生物标志物筛选过程中可用监督学习方法来充当分类器模型评估所选生物标志物的分类效果,常用方法主要有决策树与随机森林、支持向量机及正交偏最小二乘判别分析(Orthogonal partial least squares discriminant analysis,OPLS-DA)等。需要注意的是,并非所有的监督学习方法都具有特征选择的功能,这些方法需要与现有的特征选择方法联用才能用于标志物的发现[29-30]。
为了使分类器模型在训练及预测阶段能够高效利用数据,一般会将数据集分为3个部分:训练集、验证集和测试集。模型在训练集上学习样本数据,通过给定算法优化损失函数在训练集上得到较好的分类性能;之后通过验证集进一步微调模型中的参数或结构;最后在测试集进行分类预测以评估泛化能力。当样本量较少时可以不设定专门的验证集,采用十折交叉验证[31]等方式划分训练集与测试集,进行模型的训练及效能评估。
在研究之中,二元分类器应用最为广泛,其分类结果分为4类:真阳性(True positive,TP)、假阳性(False positive,FP)、真阴性(True negative,TN)、假阴性(False negative,FN)。
通常使用灵敏度(Sensitivity,Sn)、特异度(Specificity,Sp)、准确率(Accuracy,Ac)、受试者工作特征曲线下面积(Area under the receiver operating characteristic curve,AUC)[32-33]四个通用指标评价分类器的分类效果。灵敏度衡量被正确识别的阳性比例;特异度衡量被正确识别的阴性比例;准确率衡量被正确识别的样本比例。
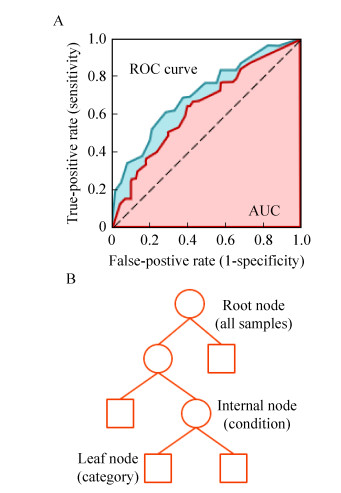
分类器模型预测过程中,样本通过计算产生一系列实数参数,通过参数与分类阈值的大小比较将各样本划分至不同的类,若改变阈值的取值,分类器模型可以获得不同的分类结果。不同阈值下可获得一系列“FPR-TPR”点,将这些点连接绘制成的曲线即为ROC曲线(Receiver operating characteristic curve),其中横坐标代表假阳性率(False positive rate),接近左上角的点对应着该分类器分类效果较好的阈值。ROC曲线与横轴构成的面积即为AUC,该值越接近于1,分类器的分类性能越好(图 4A)。
|
| 图 4 蛋白质生物标志物发现中的监督学习方法 Fig. 4 Supervised learning methods in the identification of protein biomarkers. (A) ROC curve and AUC. (B) Schematic diagram of the decision tree algorithm. All samples are divided into different categories via internal nodes |
| |
决策树是应用最为广泛的归纳推理算法之一,这种树形结构的每个叶节点都对应一种决策结果,其他的内部节点对应于一种属性测试,根节点包含样本全集(图 4B);每个节点包含的样本集合根据属性测试的结果被划分到子节点之中,我们希望随着模型划分过程的不断进行,决策树的分支节点包含的样品尽可能地处于同一类别。根据属性测试的评判标准,常见的决策树包括C4.5树(信息增益率)[34]及CART树(基尼系数)[35]。决策树形成的边界有一个明显的特点,即分类边界由若干个与轴平行的分段所构成。这种边界构成使得判断标准有极强的可解释性,因为每一段划分边界直接对应了某种属性取值,故而决策树除了充当分类器以外,也能用于进行特征选择。
单一决策树分类易产生过拟合,将决策树作为基学习器进行集成学习,即构建随机森林可以弥补这一缺点。随机森林的具体思想是对于训练数据的不同子集并行化地建立许多不同的决策树进行学习及分类,采用简单投票法作出最终的分类判断[36]。与决策树一样,随机森林可以进行具有极高可解释性的特征选择并对选出的特征进行结果评价。由于训练过程中同时考虑了样本扰动与属性扰动,相对于单一决策树,随机森林具有更强的泛化性能。随机森林分类器的分类误差主要来自于各个决策树的性能以及随机森林中树与树之间的相关性。目前随机森林已经在生物标志物发现中得到了广泛的应用,CRAN社区已推出R语言包randomForest用于随机森林预测及回归,同时支持C4.5树及CART树,并且提供变量的重要性排序及分类性能预测等核心功能。
Gao等[37]对于肝病生物标志物的研究之中,对69组正常对照(NC)、49组乙肝(HBV)、52组肝硬化(LC)及39组肝细胞癌患者(HCC)的血浆样品数据按照病程的发展进行了随机森林的二元分析,训练阶段在NC vs HBV、HBV vs LC、LC vs HCC三个阶段中均能达到100%的分类准确率,测试阶段三组的准确率分别为100%、100%及96.77%。依据对于分类性能的贡献度,分别提取前30组变量进行后续的二元逻辑回归以发现候选标志物的最佳组合,最终组合在测试集上的AUC分别能达到1.00、0.984、0.906。
Ostroff等[38]在恶性胸膜间皮瘤早期诊断的研究中,使用随机森林模型对117组病例及142组高危人群的血清蛋白质组数据进行了随机森林分类,筛选出13种炎症和增殖相关蛋白质作为生物标志物,训练、验证及测试阶段AUC分别可以达到0.99±0.01、0.98±0.04及0.95±0.04。
3.2 支持向量机支持向量机的应用基础是不同类别的样本之间线性可分,其算法核心是试图寻找最优的超平面,使得离这条线最近的异类点(即支持向量)到超平面的距离之和最大[39]。核函数、软间隔等概念的引入使得SVM拓展应用于非线性可分问题。
支持向量机被广泛用于蛋白质组数据分析且多与PCA、随机森林等其他多变量分析方法联用,在其中起到分类器的功能。SVM已有很多成熟的实现方法,在Python语言scikit-learn机器学习模块中的svm类集成了SVM分析常用的各种函数,R语言e1071包集成了LIBSVM[40]的算法。
Ahn等[41]在对胃腺癌诊断血清生物标志物的研究中,首先使用随机森林方法从对29个蛋白质进行测试的阵列平台数据中选择出重要性排序前13的蛋白质作为变量,分别以抽取不同的变量使用随机森林以及SVM的方法对患病及对照均为70组的验证集进行十次分析,二者的最高准确率分别为88.3%及89.7%;这两种算法进一步在由95个胃腺癌组和51个对照组构成的测试集上进行盲法测试,分别获得89.2%及85.6%的准确率。
Htun等[42]使用基于SVM的数据分析软件MosaCluster对急性冠状动脉综合症组及对照组的蛋白质生物标志物进行存活分析(蛋白质生物标志物由传统假设检验获得),在只使用标志物组合ACSP75时预测评价指标AUC为0.644,与Framingham Risk Score的预测结果类似(AUC=0.664);而将生物标志物组合ACSP75与先前建立的以冠状动脉疾病为特征的尿蛋白质生物标志物组合CAD238以及年龄等相关因素组合作为原始特征后,相同分类器的分类效果大大提升(AUC=0.751)。
支持向量机递归特征消除法(Support vector machine-recursive feature elimination,SVM-RFE)是一种将支持向量机与后向搜索策略相结合的包裹式特征选择方法,通过对超平面上每个特征进行排序,不断删除排名的特征并在剩余特征上进行评估,直至得到最优特征子集[43],类似的方法还包括R-SVM[44]等。但有研究表明,SVM-RFE方法选择的特征在分类过程中表现不够稳定[45-46]。
3.3 正交偏最小二乘判别分析最小二乘判别分析(PLS-DA)是PCA的回归版本,此方法的目的不在于寻找响应和独立变量之间最小方差的超平面,而是通过投影预测变量和观测变量到一个新空间通过协方差来寻找一个线性回归模型,但PLS-DA在高维度数据上倾向于构建过于复杂的模型[47],导致结果的解释性相对较差。OPLS-DA是PLS-DA的改进方法,通过引入正交信号校正(Orthogonal signal correction,OSC)滤除随机噪声,能更好地区分组间差异,具有更高的解析能力[48-49]。OPLS-DA的主要输出结果为R2与Q2,其中R2衡量拟合优度,Q2衡量模型的预测能力,越接近1效果越好[50]。R语言包“ropls”内部集成了OPLS-DA功能。
Jin等[51]在对138组膀胱癌及121组对照组成员的尿代谢组数据进行分析时,使用OPLS-DA方法进行了样本评估,包括正常组、尿血组与膀胱癌组(R2=0.878,Q2=0.662),肌肉浸润性膀胱癌组与非肌肉浸润性膀胱癌组的评估(R2=0.875,Q2=0.355);而后使用OPLS-DA方法对人工筛选的12种高相关性、灵敏度的分子在测试集(46组膀胱癌及40组对照组)上进行评估,95%置信区间上分别达到91.3%的灵敏性及92.5%的特异性,AUC为0.937。该方法还被用于年龄体重等对尿代谢组的影响效果研究[52]、血清分化胰腺癌与慢性胰腺炎的比较蛋白质组学分析[53]等工作中。
PLS-DA方法本身不具备任何的特征选择能力,需要与现有的特征选择方法联用构成完整的标志物发现流程,如Christin等[45]的工作中将PLS-DA与Rank-Product[54]方法联用,与多种标志物发现流程进行比较;Wang等[55]采用SVM-RFE类似的方法构建PLS-RFE用以微阵列数据中差异基因的筛选;Lê Cao等[31]通过在计算中引入约束项构建稀疏的偏最小二乘分析模型(Sparse PLS discriminant analysis,sPLS-DA)进行特征选择。
3.4 监督学习分类器特性比较蛋白质组学是一个相对年轻、蓬勃发展和不断扩大的领域,基于蛋白质组数据进行生物标志物发现尚未形成公认的通用数据分析流程,理解方法的使用条件显得尤其重要。基于文献调研[12, 46, 56-58]与使用经验,本文从缺失值容忍、分类能力、(对离群值的)鲁棒性、避免过拟合、降维、可解释性及可视化7个方面对3种分类器进行特性比较(表 2)。
| Characteristics | RF | SVM | OPLS-DA |
| Avoid overfitting | +++ | +++ | ++ |
| Classification ability | +++ | [+, +++]b | +++ |
| Dimensionality reduction | + | +++ | +++ |
| Interpretable | +++ | + | + |
| Missing value tolerance | +++ | + | + |
| Robustness | +++ | +++ | ++ |
| Visualization | + | +++ | +++ |
| a: +++ means the best performance, + means the worst performance; b: the classification ability of SVM is affected by the kernel function used. There are multiple kernel functions, such as linear, nonlinear, polynomial, radial basis function (RBF), and sigmoid. | |||
随机森林在分类可解释性及缺失值容忍程度上具有无可比拟的优势,而SVM和OPLS-DA在可视化等方面更加优秀,数据分析时往往需要综合考虑数据维度及数据量等因素之后选用合理的分类器。将多种分类器作为基学习器进行集成学习亦是一种可行的研究策略,相较于使用单一分类器往往能够获得更佳的泛化性能[59-60]。
3.5 监督学习常用分析工具我们在表 3中列出了实现RF、SVM及PLS-DA三类监督学习算法的常用分析工具及相关属性。
| Function | Software | Client | Platform | Link |
| PLS-DA | SIMCA-P | Local | Windows | https://umetrics.com/products/simca |
| PLS-DA | PLS Toolbox | Local | Windows/MacOS/Linux (MATLAB) | http://www.eigenvector.com/software/pls_toolbox.htm |
| SVM | LIBSVM[40] | Local | Windows/MacOS/Linux | https://www.csie.ntu.edu.tw/~cjlin/libsvm/ |
| SVM | SVM light | Local | Windows/MacOS/Linux | http://svmlight.joachims.org/ |
| SVM | SVMTorch[61] | Local | Windows/MacOS/Linux | http://bengio.abracadoudou.com/SVMTorch.html |
| RF | XLSTAT | Local | Windows (Excel) | https://www.xlstat.com/en/ |
| All | WEKA[28] | Local | Windows/MacOS/Linux | https://www.cs.waikato.ac.nz/ml/weka/ |
深度学习(Deep learning)是近年来随着硬件及算法的进步兴起的一类机器学习方法,模型的计算结构由多个处理层组成的(图 5)。在每一层中,它通过简单但是非线性的模块将原始数据转换为更高层次、更抽象的表达,这种多层结构赋予了模型更强的抽象化及特征表示的能力[62]。这是一个快速发展的研究领域,大量新的深度学习模型与框架不断被提出,这为深度学习在生物学领域的应用提供了契机。
|
| 图 5 深度学习模型示意图 Fig. 5 Schematic diagram of the deep learning model. |
| |
在深度学习方法用于鸟枪法筛选候选生物标志物方面,目前未见到相关文献报道,但稀疏自编码器[63]等深度学习模型在降噪方面的应用已有报道,可以为蛋白质生物标志物的发现提供借鉴。通过文献检索发现已有少数工作在使用生物标志物评价分类器分类效果,Putin等[58]在研究衰老生物标志物的工作中,采用62 419组健康人的血液生化分析记录(内含对应的年龄、性别及46种标准化的血液标记)作为数据集,按照训练集56 177组与测试集6 242组的比例分开,年龄、性别分别作为标签,46条标记记录作为输入值,分别在深层神经网络、决策树、随机森林、线性回归、K最近邻分类及支持向量机多种模型上进行分类性能评估,在两标签的预测中深层神经网络均取得最好的分类效果。
虽然深度学习算法在复杂和噪声数据的识别、分类和特征提取方面表现出一定优势,但也存在一些局限性。主要包括4个方面[64]:1)“黑箱”问题。多数的深度学习模型通过中间层学习高维度特征以实现分类或者预测功能,这些抽象特征需要进行额外的质量控制和解释。2)训练集规模不足时易过拟合。深度学习模型的优势往往在大数据量的情况下才会体现出来。数据量较小时,模型面临过拟合风险,将在训练集上训练的模型应用到新的数据上时易有较大误差。尽管目前已经提出L2约束项及dropout等正则化方法应对过拟合,增大训练集数据量依旧是解决此问题的根本途径。3)深度学习模型的选择。由于可供选择的深度学习模型众多,再加上数据类型和数据量等要求,对于特定任务选择哪类模型进行训练并不像选择传统机器学习算法那么直观。4)计算成本。尽管训练深度学习模型所需的计算资源并没有想象中的那么大,但训练过程通常涉及密集又耗时的计算,因此常需要使用图形处理单元(GPU)进行并行加速。
5 总结与展望目前,基于蛋白质组数据进行蛋白质生物标志物的发现已经取得了长足的进步。本文全面阐述了蛋白质生物标志物的发现策略,常用特征选择及机器学习方法的原理及适用范围,并讨论了深度学习在本领域的应用合理性及局限性。具体内容总结为以下5点:1)蛋白质生物标志物筛选本质上是特征选择与分类器效能评估问题。传统的假设检验及回归分析受到变量相关性、分类边界等问题的限制,不适用于现有的标志物发现策略;不过,已有一些机器学习方法可以解决上述问题。2)无监督学习方法在标志物发现中可用于数据异常值检验、数据重复性分析、结果可视化呈现及标志物分离结果的检验;监督学习方法主要作为分类器用以评估蛋白质生物标志物组合的分类效果,一些不具备特征选择功能的方法需要与现有特征选择方法联用才能进行完整的生物标志物发现。3)监督学习分类器使用时需将数据集划分为训练集、验证集及测试集,常使用灵敏度、特异度、准确率及AUC评判分类效果。4)不同的分类器适用条件不同,选择过程需要综合考虑数据维度及数据量等因素。将多种分类器作为基学习器进行集成学习也是一种可行的研究策略,相较于单一分类方法往往能够获得更佳的泛化性能。5)深度学习作为新兴起的一门技术,在标志物分类效果评估方面已有初步应用。虽有“黑箱”、过拟合、模型选择及计算成本等问题需要解决,但随着相关技术的进步,深度学习在生物标志物筛选方面仍有着很好的应用前景。
虽然早期蛋白质生物标志物筛选工作中,研究者倾向于获得一种特定的蛋白质作为生物标志物,但最近有研究表明将多个现有标志物进行组合形成新的评判指标能有效提升预测准确性[65-66]。目前已有Child-Pugh score[67]、Framingham Risk Score[68]、OVA1 test[69]等多种组合标志物应用于临床诊断,将多种标志物定量结果组合形成综合性的评判指标已成为研究的主流趋势。此外,将多组学数据综合分析寻找标志物也逐渐成为研究热点,Cohen等[70]将ctDNA与8种已知的血浆生物标志物共同分析进行的早期癌症检测(该方法称为CancerSEEK),在生物标志物发现领域引起了极大反响;Sinha等[71]通过对前列腺癌蛋白质、mRNA、甲基化、组蛋白修饰及拷贝数变异等诸多因素的综合分析,认为组学间无法相互取代,多组学来源的生物标志物的组合相较单一来源的生物标志物更为准确。这些都对从事生物标志物筛选的人员提出了更高的要求,一方面应尝试更多特征选择和分类方法的组合,尝试多种分析手段集成分析,以获得更好的分类效果;另一方面,在标志物发现领域数据分析的工作量依旧非常大,目前仍缺少更为方便的一体化数据分析平台。
| [1] |
Biomarkers Definitions Working Group. Biomarkers and surrogate endpoints: preferred definitions and conceptual framework. Clin Pharmacol Ther, 2001, 69(3): 89-95. DOI:10.1067/mcp.2001.113989 |
| [2] |
Etzioni R, Urban N, Ramsey S, et al. The case for early detection. Nat Rev Cancer, 2003, 3(4): 243-252. DOI:10.1038/nrc1041 |
| [3] |
FDA-NIH Biomarker Working Group. BEST (Biomarkers, EndpointS, and other Tools) Resource. Silver Spring: Food and Drug Administration (US), 2016: 48.
|
| [4] |
Mischak H, Allmaier G, Apweiler R, et al. Recommendations for biomarker identification and qualification in clinical proteomics. Sci Transl Med, 2010, 2(46): 46ps42. |
| [5] |
Ludwig JA, Weinstein JN. Biomarkers in cancer staging, prognosis and treatment selection. Nat Rev Cancer, 2005, 5(11): 845-856. DOI:10.1038/nrc1739 |
| [6] |
Kuster B, Schirle M, Mallick P, et al. Scoring proteomes with proteotypic peptide probes. Nat Rev Mol Cell Biol, 2005, 6(7): 577-583. DOI:10.1038/nrm1683 |
| [7] |
Bekker-Jensen DB, Kelstrup CD, Batth TS, et al. An optimized shotgun strategy for the rapid generation of comprehensive human proteomes. Cell Syst, 2017, 4(6): 587-599. DOI:10.1016/j.cels.2017.05.009 |
| [8] |
Mann M, Kulak NA, Nagaraj N, et al. The coming age of complete, accurate, and ubiquitous proteomes. Mol Cell, 2013, 49(4): 583-590. DOI:10.1016/j.molcel.2013.01.029 |
| [9] |
Sharma K, Schmitt S, Bergner CG, et al. Cell type- and brain region-resolved mouse brain proteome. Nat Neurosci, 2015, 18(12): 1819-1831. DOI:10.1038/nn.4160 |
| [10] |
Richards AL, Merrill AE, Coon JJ. Proteome sequencing goes deep. Curr Opin Chem Biol, 2015, 24: 11-17. DOI:10.1016/j.cbpa.2014.10.017 |
| [11] |
Geyer PE, Holdt LM, Teupser D, et al. Revisiting biomarker discovery by plasma proteomics. Mol Syst Biol, 2017, 13(9): 942. DOI:10.15252/msb.20156297 |
| [12] |
Swan AL, Mobasheri A, Allaway D, et al. Application of machine learning to proteomics data: classification and biomarker identification in postgenomics biology. OMICS, 2013, 17(12): 595-610. DOI:10.1089/omi.2013.0017 |
| [13] |
Rifai N, Gillette MA, Carr SA. Protein biomarker discovery and validation: the long and uncertain path to clinical utility. Nat Biotechnol, 2006, 24(8): 971-983. DOI:10.1038/nbt1235 |
| [14] |
Guyon I, Elisseeff A. An introduction to variable and feature selection. J Mach Learn Res, 2003, 3: 1157-1182. |
| [15] |
Suppers A, Van Gool AJ, Wessels HJCT. Integrated chemometrics and statistics to drive successful proteomics biomarker discovery. Proteomes, 2018, 6(2): 20. DOI:10.3390/proteomes6020020 |
| [16] |
Maes E, Kelchtermans P, Bittremieux W, et al. Designing biomedical proteomics experiments: state-of-the-art and future perspectives. Expert Rev Proteomics, 2016, 13(5): 495-511. DOI:10.1586/14789450.2016.1172967 |
| [17] |
Hoque N, Bhattacharyya DK, Kalita JK. MIFS-ND: a mutual information-based feature selection method. Expert Syst Appl, 2014, 41(14): 6371-6385. DOI:10.1016/j.eswa.2014.04.019 |
| [18] |
Robnik-Šikonja M, Kononenko I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach Learn, 2003, 53(1/2): 23-69. DOI:10.1023/A:1025667309714 |
| [19] |
Radovic M, Ghalwash M, Filipovic N, et al. Minimum redundancy maximum relevance feature selection approach for temporal gene expression data. BMC Bioinformatics, 2017, 18: 9. DOI:10.1186/s12859-016-1423-9 |
| [20] |
Shen SH, Gui TT, Ma CC. Identification of molecular biomarkers for pancreatic cancer with mRMR shortest path method. Oncotarget, 2017, 8(25): 41432-41439. |
| [21] |
Blanchet L, Smolinska A, Attali A, et al. Fusion of metabolomics and proteomics data for biomarkers discovery: case study on the experimental autoimmune encephalomyelitis. BMC Bioinformatics, 2011, 12: 254. DOI:10.1186/1471-2105-12-254 |
| [22] |
Zhang L, Xiao H, Karlan S, et al. Discovery and preclinical validation of salivary transcriptomic and proteomic biomarkers for the non-invasive detection of breast cancer. PLoS ONE, 2010, 5(12): e15573. DOI:10.1371/journal.pone.0015573 |
| [23] |
Govorukhina NI, Reijmers TH, Nyangoma SO, et al. Analysis of human serum by liquid chromatography-mass spectrometry: improved sample preparation and data analysis. J Chromatogr A, 2006, 1120(1/2): 142-150. |
| [24] |
Liggett WS, Barker PE, Semmes OJ, et al. Measurement reproducibility in the early stages of biomarker development. Dis Markers, 2004, 20(6): 295-307. DOI:10.1155/2004/726517 |
| [25] |
de Wit M, Kant H, Piersma SR, et al. Colorectal cancer candidate biomarkers identified by tissue secretome proteome profiling. J Proteomics, 2014, 99: 26-39. DOI:10.1016/j.jprot.2014.01.001 |
| [26] |
Griffin NM, Yu JY, Long F, et al. Label-free, normalized quantification of complex mass spectrometry data for proteomic analysis. Nat Biotechnol, 2010, 28(1): 83-89. |
| [27] |
Metsalu T, Vilo J. ClustVis: a web tool for visualizing clustering of multivariate data using principal component analysis and heatmap. Nucleic Acids Res, 2015, 43: W566-W570. DOI:10.1093/nar/gkv468 |
| [28] |
Frank E, Hall M, Trigg L, et al. Data mining in bioinformatics using Weka. Bioinformatics, 2004, 20(15): 2479-2481. DOI:10.1093/bioinformatics/bth261 |
| [29] |
Smit S, van Breemen MJ, Hoefsloot HCJ, et al. Assessing the statistical validity of proteomics based biomarkers. Anal Chim Acta, 2007, 592(2): 210-217. DOI:10.1016/j.aca.2007.04.043 |
| [30] |
Smit S, Hoefsloot HCJ, Smilde AK. Statistical data processing in clinical proteomics. J Chromatogr B Analyt Technol Biomed Life Sci, 2008, 866(1/2): 77-88. |
| [31] |
Lê Cao KA, Boitard S, Besse P. Sparse PLS discriminant analysis: biologically relevant feature selection and graphical displays for multiclass problems. BMC Bioinformatics, 2011, 12: 253. DOI:10.1186/1471-2105-12-253 |
| [32] |
Lobo JM, Jiménez-Valverde A, Real R. AUC: a misleading measure of the performance of predictive distribution models. Glob Ecol Biogeogr, 2008, 17(2): 145-151. DOI:10.1111/geb.2008.17.issue-2 |
| [33] |
Austin PC, Steyerberg EW. Interpreting the concordance statistic of a logistic regression model: relation to the variance and odds ratio of a continuous explanatory variable. BMC Med Res Methodol, 2012, 12: 82. DOI:10.1186/1471-2288-12-82 |
| [34] |
Quinlan JR. C4.5: Programs for Machine Learning. San Francisco: Morgan Kaufmann Publishers, 1993.
|
| [35] |
Breiman L, Friedman JH, Olshen RA, et al. Classification and Regression Trees. New York: Chapman & Hall, 1984: 582-588.
|
| [36] |
Yang PY, Yang YH, Zhou BB, et al. A review of ensemble methods in bioinformatics. Curr Bioinf, 2010, 5(4): 296-308. DOI:10.2174/157489310794072508 |
| [37] |
Gao R, Cheng JH, Fan CL, et al. Serum metabolomics to identify the liver disease-specific biomarkers for the progression of hepatitis to hepatocellular carcinoma. Sci Rep, 2015, 5: 18175. DOI:10.1038/srep18175 |
| [38] |
Ostroff RM, Mehan MR, Stewart A, et al. Early detection of malignant pleural mesothelioma in asbestos-exposed individuals with a noninvasive proteomics-based surveillance tool. PLoS ONE, 2012, 7(10): e46091. DOI:10.1371/journal.pone.0046091 |
| [39] |
Cortes C, Vapnik V. Support-vector networks. Mach Learn, 1995, 20(3): 273-297. |
| [40] |
Chang CC, Lin CJ. LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol, 2011, 2(3): Article No.27.
|
| [41] |
Ahn HS, Shin YS, Park PJ, et al. Serum biomarker panels for the diagnosis of gastric adenocarcinoma. Br J Cancer, 2012, 106(4): 733-739. DOI:10.1038/bjc.2011.592 |
| [42] |
Htun NM, Magliano DJ, Zhang ZY, et al. Prediction of acute coronary syndromes by urinary proteome analysis. PLoS ONE, 2017, 12(3): e0172036. DOI:10.1371/journal.pone.0172036 |
| [43] |
Guyon I, Weston J, Barnhill S, et al. Gene selection for cancer classification using support vector machines. Mach Learn, 2002, 46(1/3): 389-422. DOI:10.1023/A:1012487302797 |
| [44] |
Zhang XG, Lu X, Shi Q, et al. Recursive SVM feature selection and sample classification for mass-spectrometry and microarray data. BMC Bioinformatics, 2006, 7: 197. DOI:10.1186/1471-2105-7-197 |
| [45] |
Christin C, Hoefsloot HCJ, Smilde AK, et al. A critical assessment of feature selection methods for biomarker discovery in clinical proteomics. Mol Cell Proteomics, 2013, 12(1): 263-276. DOI:10.1074/mcp.M112.022566 |
| [46] |
Swan AL, Stekel DJ, Hodgman C, et al. A machine learning heuristic to identify biologically relevant and minimal biomarker panels from omics data. BMC Genomics, 2015, 16(Suppl 1): S2. DOI:10.1186/1471-2164-16-S1-S2 |
| [47] |
Bylesjö M, Rantalainen M, Cloarec O, et al. OPLS discriminant analysis: combining the strengths of PLS‐DA and SIMCA classification. J Chemom, 2006, 20(8/10): 341-351. |
| [48] |
Worley B, Powers R. Multivariate analysis in metabolomics. Curr Metabolomics, 2013, 1(1): 92-107. |
| [49] |
Pinto RC, Trygg J, Gottfries J. Advantages of orthogonal inspection in chemometrics. J Chemom, 2012, 26(6): 231-235. DOI:10.1002/cem.v26.6 |
| [50] |
Triba MN, Le Moyec L, Amathieu R, et al. PLS/OPLS models in metabolomics: the impact of permutation of dataset rows on the K-fold cross-validation quality parameters. Mol BioSyst, 2015, 11(1): 13-19. DOI:10.1039/C4MB00414K |
| [51] |
Jin X, Yun SJ, Jeong P, et al. Diagnosis of bladder cancer and prediction of survival by urinary metabolomics. Oncotarget, 2014, 5(6): 1635-1645. |
| [52] |
Thevenot EA, Roux A, Xu Y, et al. Analysis of the human adult urinary metabolome variations with age, body mass index, and gender by implementing a comprehensive workflow for univariate and OPLS statistical analyses. J Proteome Res, 2015, 14(8): 3322-3335. DOI:10.1021/acs.jproteome.5b00354 |
| [53] |
Saraswat M, Joenväärä S, Seppänen H, et al. Comparative proteomic profiling of the serum differentiates pancreatic cancer from chronic pancreatitis. Cancer Med, 2017, 6(7): 1738-1751. DOI:10.1002/cam4.2017.6.issue-7 |
| [54] |
Breitling R, Armengaud P, Amtmann A, et al. Rank products: a simple, yet powerful, new method to detect differentially regulated genes in replicated microarray experiments. FEBS Lett, 2004, 573(1/3): 83-92. |
| [55] |
Wang AG, An N, Chen GL, et al. Improving PLS-RFE based gene selection for microarray data classification. Comput Biol Med, 2015, 62: 14-24. DOI:10.1016/j.compbiomed.2015.04.011 |
| [56] |
Gromski PS, Muhamadali H, Ellis DI, et al. A tutorial review: metabolomics and partial least squares-discriminant analysis-a marriage of convenience or a shotgun wedding. Anal Chim Acta, 2015, 879: 10-23. DOI:10.1016/j.aca.2015.02.012 |
| [57] |
Sampson DL, Parker TJ, Upton Z, et al. A comparison of methods for classifying clinical samples based on proteomics data: a case study for statistical and machine learning approaches. PLoS ONE, 2011, 6(9): e24973. DOI:10.1371/journal.pone.0024973 |
| [58] |
Putin E, Mamoshina P, Aliper A, et al. Deep biomarkers of human aging: application of deep neural networks to biomarker development. Aging (Albany NY), 2016, 8(5): 1021-1033. |
| [59] |
Ge GT, Wong GW. Classification of premalignant pancreatic cancer mass-spectrometry data using decision tree ensembles. BMC Bioinformatics, 2008, 9: 275. DOI:10.1186/1471-2105-9-275 |
| [60] |
He S, Chen HH, Zhu ZX, et al. Robust twin boosting for feature selection from high-dimensional omics data with label noise. Inf Sci (NY), 2015, 291: 1-18. DOI:10.1016/j.ins.2014.08.048 |
| [61] |
Collobert R, Bengio S. SVMTorch: support vector machines for large-scale regression problems. J Mach Learn Res, 2001, 1(2): 143-160. |
| [62] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [63] |
Vincent P, Larochelle H, Bengio Y, et al. Extracting and Composing Robust Features with Denoising Autoencoders//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland: ACM, 2008.
|
| [64] |
Mamoshina P, Vieira A, Putin E, et al. Applications of deep learning in biomedicine. Mol Pharm, 2016, 13(5): 1445-1454. DOI:10.1021/acs.molpharmaceut.5b00982 |
| [65] |
Mazzara S, Rossi RL, Grifantini R, et al. CombiROC: an interactive web tool for selecting accurate marker combinations of omics data. Sci Rep, 2017, 7: 45477. DOI:10.1038/srep45477 |
| [66] |
Kulasingam V, Diamandis EP. Strategies for discovering novel cancer biomarkers through utilization of emerging technologies. Nat Clin Pract Oncol, 2008, 5(10): 588-599. DOI:10.1038/ncponc1187 |
| [67] |
Cholongitas E, Papatheodoridis GV, Vangeli M, et al. Systematic review: the model for end-stage liver disease--should it replace Child-Pugh's classification for assessing prognosis in cirrhosis?. Aliment Pharmacol Ther, 2005, 22(11/12): 1079-1089. |
| [68] |
D'Agostino RB Sr, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the framingham heart study. Circulation, 2008, 117(6): 743-753. DOI:10.1161/CIRCULATIONAHA.107.699579 |
| [69] |
Fung ET. A recipe for proteomics diagnostic test development: the OVA1 test, from biomarker discovery to FDA clearance. Clin Chem, 2010, 56(2): 327-329. DOI:10.1373/clinchem.2009.140855 |
| [70] |
Cohen JD, Li L, Wang YX, et al. Detection and localization of surgically resectable cancers with a multi-analyte blood test. Science, 2018, 359(6378): 926-930. DOI:10.1126/science.aar3247 |
| [71] |
Sinha A, Huang V, Livingstone J, et al. The proteogenomic landscape of curable prostate cancer. Cancer Cell, 2019, 35(3): 414-427.e6. DOI:10.1016/j.ccell.2019.02.005 |
 2019, Vol. 35
2019, Vol. 35