2022, Vol. 38
表1(Table 1)
13C标记代谢流分析中天然稳定性同位素修正矩阵构建方法及应用
http://dx.doi.org/10.13345/j.cjb.220081
中国科学院微生物研究所、中国微生物学会主办
中国科学院微生物研究所、中国微生物学会主办
文章信息
- 郑世媛, 江俊峰, 夏建业
- ZHENG Shiyuan, JIANG Junfeng, XIA Jianye
- 13C标记代谢流分析中天然稳定性同位素修正矩阵构建方法及应用
- Construction and application of natural stable isotope correction matrix in 13C-labeled metabolic flux analysis
- 生物工程学报, 2022, 38(10): 3940-3955
- Chinese Journal of Biotechnology, 2022, 38(10): 3940-3955
- 10.13345/j.cjb.220081
-
文章历史
- Received: January 30, 2022
- Accepted: March 28, 2022
- Published: March 31, 2022
引用本文
|
郑世媛, 江俊峰, 夏建业, 等. 13C标记代谢流分析中天然稳定性同位素修正矩阵构建方法及应用. 生物工程学报, 2022, 38(10): 3940-3955.
ZHENG SY, JIANG JF, XIA JY, et al. Construction and application of natural stable isotope correction matrix in 13C-labeled metabolic flux analysis. Chinese Journal of Biotechnology, 2022, 38(10): 3940-3955.
13C标记代谢流分析中天然稳定性同位素修正矩阵构建方法及应用
1. 华东理工大学 生物反应器工程国家重点实验室, 上海 200237;
2. 中国科学院天津工业生物技术研究所, 天津 300308
2. 中国科学院天津工业生物技术研究所, 天津 300308
摘要：稳定性同位素13C标记实验是分析细胞代谢流的一种重要手段，主要通过质谱检测胞内代谢物中13C标记的同位素分布，并作为胞内代谢流计算时的约束条件，进而通过代谢流分析算法得到相应代谢网络中的通量分布。然而在自然界中，并非只有C元素存在天然稳定性同位素13C，其他元素如O元素也有其天然稳定性同位素17O、18O等，这使得质谱方法所测得的同位素分布中会夹杂除13C标记之外的其他元素的同位素信息，特别是分子中含有较多其他元素的分子，这将导致很大的实验误差，因此需要在进行代谢流计算前进行质谱数据的矫正。本研究提出了一种基于Python语言的天然同位素修正矩阵的构建方法，用于修正同位素分布测量值中由于天然同位素分布引起的测定误差。文中提出的基本修正矩阵幂方法用于构建各元素修正矩阵，结构简单、易于编码实现，可直接应用于13C代谢流分析软件数据前处理。将该修正方法应用于13C标记的黑曲霉(Aspergillus niger) 胞内代谢流分析，结果表明本研究提出的方法准确有效，为准确获取微生物胞内代谢流分析提供了可靠的数据修正方法。
关键词：代谢流分析 天然同位素修正矩阵 质谱分析 Python
Construction and application of natural stable isotope correction matrix in 13C-labeled metabolic flux analysis
1. State Key Laboratory of Bioreactor Engineering, East China University of Science and Technology, Shanghai, 200237, China;
2. Tianjin Institute of Industrial Biotechnology, Chinese Academy of Science, Tianjin 300308, China
2. Tianjin Institute of Industrial Biotechnology, Chinese Academy of Science, Tianjin 300308, China
Abstract: Stable isotope 13C labeling is an important tool to analyze cellular metabolic flux. The 13C distribution in intracellular metabolites can be detected via mass spectrometry and used as a constraint in intracellular metabolic flux calculations. Then, metabolic flux analysis algorithms can be employed to obtain the flux distribution in the corresponding metabolic reaction network. However, in addition to carbon, other elements such as oxygen in the nature also have natural stable isotopes (e.g., 17O, 18O). This makes the isotopic information of elements other than the 13C marker interspersed in the isotopic distribution measured by the mass spectrometry, especially that of the molecules containing many other elements, which leads to large errors. Therefore, it is essential to correct the mass spectrometry data before performing metabolic flux calculations. In this paper, we proposed a method for construction of correction matrix based on Python language for correcting the measurement errors due to natural isotope distribution. The method employed a basic power method for constructing the correction matrix with simple structure and easy coding implementation, which can be directly applied to data pre-processing in 13C metabolic flux analysis. The correction method was then applied to the intracellular metabolic flux analysis of 13C-labeled Aspergillus niger. The results showed that the proposed method was accurate and effective, which can serve as a reliable data correction method for accurate microbial intracellular metabolic flux analysis.
Keywords:
metabolic flux analysis natural isotope correction matrix mass spectrometry Python
代谢流组学能够直接反映细胞的代谢状态，是研究微生物细胞代谢特性的重要工具。然而代谢流作为反应速率是无法通过电极进行直接检测的，必须根据质量平衡或同位素平衡的基本原理，利用计算模型估计代谢反应通量[1-3]。在这些代谢通量计算方法中，基于同位素13C的代谢通量分析(13C-mass flux analysis, 13C-MFA) 目前被认为是获得微生物在特定稳态[4-5]或动态条件[6]下胞内代谢通量的标准方法[2, 7-8]。用13C标记的底物喂养微生物细胞，代谢途径不同中间产物分子中13C/12C比率将随着时间的推移而被检测出来，这些信息可以被用以获取不同途径的相对反应通量比率[9-10]。以这些代谢物的同位素标记信息(mass distribution vector, MDV) 作为约束，使用13C-MFA算法计算细胞内的代谢通量(如MSCorr[11]、ICT[12]、IsoCor[13])。然而，从质谱原始文件中得到的MDV值不能直接用于13C-MFA软件，因为中间代谢物分子中除实验标记用C原子外其他元素原子的天然稳定同位素(如17O、15N) 丰度会给这些MDV带来偏差[14]。由于大多数有机物分子中相关元素也可能具有两种或两种以上的稳定同位素(表 1)，因此需要对质谱测定的原始MDV进行修正以计算准确的代谢通量[15]。Niedenführ等[16]从算法逻辑以及实际应用(包括13C代谢流分析和同位素稀释质谱) 上验证了天然同位素会对代谢流计算的通量分布产生影响，得出了基于同位素的通量组学和定量代谢组学中的自然丰度修正对于正确解释实验数据至关重要的结论。
表 1 自然界中稳定同位素的分布概率
Table 1 Distribution probabilities of stable isotopes in the nature
| Element | Stable isotopes | Corresponding abundance of each isotope | |||
| Carbon | 12C, 13C | 0.988 9 | 0.011 1 | ||
| Hydrogen | 1H, 2H | 0.999 9 | 0.000 1 | ||
| Nitrogen | 14N, 15N | 0.996 3 | 0.003 7 | ||
| Oxygen | 16O, 17O, 18O | 0.997 6 | 0.000 4 | 0.002 0 | |
| Silicon | 28Si, 29Si, 30Si | 0.922 3 | 0.046 8 | 0.002 0 | |
| Sulfur | 32S, 33S, 34S, 36S | 0.949 3 | 0.007 6 | 0.042 9 | 0.000 2 |
目前已被应用于实践的天然同位素修正方法有：由MATLAB编写的软件MSCorr[11]，基于Perl语言编写的修正软件ICT[12]，以及包含了57Fe和77Se等不常见原子天然同位素修正软件IsoCor[13]，用于双同位素示踪剂实验的同位素自然丰度校正的AccuCor2[17]。以上所提及的方法各有优缺点，MSCorr优先提出使用算法解决天然同位素修正的问题，但所支持的示踪剂只限于13C和15N；IsoCor支持修正未标记位置的示踪剂的自然丰度，但无法修正来自串联质谱的实验数据[12, 18]；ICT支持修正来自串联质谱的离子碎片自然丰度，但其修正过程与代谢流分析相分离，使得代谢流分析过程变得复杂；AccuCor2只能校正C和H两种元素的天然同位素。以上算法的一个共同点就是，均采用复杂数学表达式表示算法过程。尽管以上算法开源，但由于难于理解，在应用于自主13C-MFA分析软件开发时，很难判断导致代谢流计算偏差的根源到底在哪里。因此亟需一种构建方法简单、易于理解、方便代码编制的算法，来进行天然同位素分布修正矩阵的构建。
为解决以上问题，我们在这项工作中提出了一种基于修正矩阵分离及元素修正矩阵概念的修正矩阵构建方法，并基于该方法实现了Python代码编制，所实现的代码可以很容易地嵌入或集成到13C-MFA软件中。最后通过将文中提出方法应用于黑曲霉(Aspergillus niger) 不同条件下代谢流分析中，验证了该方法的有效性和可靠性，为构建基于13C标记的MFA软件平台奠定了基础。
1 方法与原理 1.1 传统方法常见有机物分子中各元素的天然同位素分布如表 1所示，从表中可以看出有些元素如C、H只有两种天然同位素，而S的天然同位素多达4种，这种情况下，按照传统方法[19]计算就增加了工作量。
传统的矩阵修正方法[19]如公式(1) 所示，A表示的是某一元素在某化合物中的天然同位素分布概率。假设该元素共有N个天然同位素I(1)、I(2)……I(N)，这些同位素在自然界中的丰度分布概率为p(I(1))、p(I(2))……p(I(N))，在这个化合物中该元素原子出现的次数为f(I(1))、f(I(2))……f(I(N))。这种方法计算过程较烦琐，且对单一元素的天然同位素分布进行修正之后，还需另外将所有元素的同位素分布进行卷积求解修正后化合物的MDV分布，因此本文提出了更加简洁的计算方法，弥补了传统方法的缺点。
|
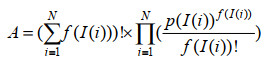
(1) |
有研究表明[15]，天然同位素修正的基本原理可以解释为公式(2)：
|
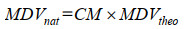
(2) |
其中，MDV为待测样品分子中某一种代谢物所有同位素异构体比例构成的向量。MDVtheo代表该代谢物分子中仅存在示踪稳定性同位素(例如13C-MFA中加入的13C) 时形成的同位素异构体构成的MDV，MDVnat代表该代谢物中由于实际掺杂其他元素的天然同位素(如17O和15N等) 而在质谱中实际测定的MDV。修正矩阵(correction matrix, CM) 代表的是需要构建的修正矩阵。下面以葡萄糖(C6H12O6) 分子为例说明本文构建CM的方法。
以天然葡萄糖分子为例，其质谱(mass spectrum, MS) 不仅包含m/z=180的峰，还包含其他的峰：如m/z=181 (M+1)、182 (M+2) 等，这是因为分子中存在各元素天然同位素13C (含量1.107%)、2H (含量0.012%)、17O (含量0.038%)、18O (含量0.205%)。理论上，葡萄糖分子的质谱峰图一共有31个峰。实际上由于分子中稀缺同位素组合的丰度低于目前MS系统的检测限，一般的MS系统只能检测到6个峰或更少。如果我们将U-13C标记的葡萄糖和天然葡萄糖以1︰2的比例混合，理论上不考虑天然同位素影响时MS谱中得到两个峰，即M+0 (天然葡萄糖) 和M+6 (U-13C标记的葡萄糖)，它们的离子流强度比为2︰1。然而，由于天然同位素的存在，将得到远多于两个峰。因此，我们需要消除天然同位素的干扰，将理论MDV比值输入13C-MFA软件进行代谢通量分析。这个步骤被称为天然同位素修正。
以葡萄糖分子为例，其分子中有6个碳原子、12个氢原子和6个氧原子，MDVnat可以表示为：
|
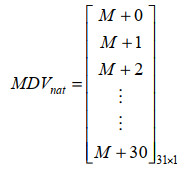
(3) |
该向量中的每一行代表一个同位素异构体质量同位素分布(mass isotope distribution, MID)[20]的比例，例如，M+0描述的是含有6个12C、12个1H和6个16O的同位素异构体的比例，而M+1则代表含有一个额外原子质量的葡萄糖分子(这可能是一个12C替换为13C，或一个1H替换为2H，或一个16O替换为17O)。因此，MDVnat应该被修正，以消除由其他元素天然同位素如2H、17O和18O引入的额外质量。通过自然同位素修正得到MDVtheo，它只包括示踪剂中13C标记的葡萄糖分子的贡献。
MDVnat矢量的行数由式(4) 确定：
|
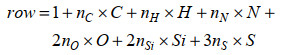
(4) |
其中ni代表i元素在分子中的原子个数。
1.3 修正矩阵分解与元素本元修正矩阵MDVnat和MDVtheo之间的关系表示为公式(2)：
其中CM为方阵行数与MDV行数相同，利用修正矩阵CM可以在MDVnat和MDVtheo之间进行转换。与其他构建修正矩阵的方法不同，本文中提出修正矩阵元素分解和元素本元修正矩阵的概念。修正矩阵元素分解即根据各元素修正互不干扰的特点可将CM分解为各元素本元修正矩阵CMi (i代表各元素)。本文将修正矩阵分解为各元素本元修正矩阵幂的矩阵乘积，如式(5) 所示。
|
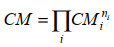
(5) |
其中CMi代表元素i的本元修正矩阵，幂ni是分子中元素i的原子数。本元修正矩阵是由该元素天然同位素分布向量构建而成，因此称为本元修正矩阵。
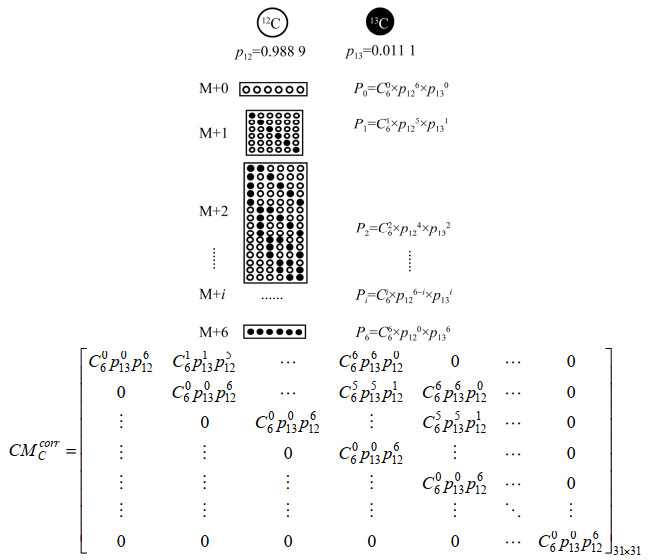
以下以葡萄糖分子为例，详细介绍以上矩阵分解的基本原理，并分别介绍各元素本元修正矩阵及修正矩阵元素分解的概念及构建过程。葡萄糖分子中共有6个C原子、12个H原子及6个O原子。根据排列组合中乘法原理，可将修正过程分解为依次进行的各元素修正，据此CM可分解为各元素对应修正矩阵的乘积。而各元素的修正矩阵由其在葡萄糖分子中的原子个数及其天然同位素分布信息决定，以葡萄糖分子中的C原子为例，其对应的修正矩阵的构造可由图 1表示。
|
| 图 1 葡萄糖分子中以C原子为例的修正矩阵构造方法 Fig. 1 Construction of correction matrix for carbon in glucose. 其中○表示12C原子，●表示13C原子，p表示每个碳原子位置上出现12C或13C的概率，P表示每种MDV可能出现的概率，图中所示为M+0、M+1、M+2三种组合各自出现的概率。其中M+2将多种可能的组合合并为一组概率，这样的好处是大大减少了计算量，同时又能覆盖到所有可能的组合，图中用CMCcorr表示C元素的修正矩阵 ○ denotes 12C, ● denotes 13C, p denotes the probability of occurrence of 12C or 13C at each carbon atomic position, and P denotes the probability of occurrence of each possible MDV, with the probabilities of occurrence of three combinations M+0, M+1, M+2 shown in the figure. To be noted that M+2 combines multiple possible combinations into one set of probabilities, which has the advantage of greatly reducing the computational effort while covering all possible combinations, the correction matrix of C elements is denoted by CMCcorr in the figure. |
| |
从图 1可见，CMCcorr为上三角方阵，根据矩阵乘法原理，该方阵可分解为以下矩阵的6次幂，即
|
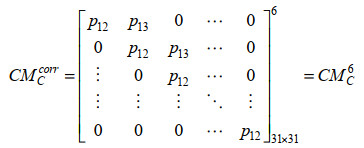
(6) |
式中定义的CMC称为葡萄糖分子中C元素的本元修正矩阵，并且有
|
(7) |
因此便可得到式(5) 所示修正矩阵的分解，对应的公式(2) 即转化为：
|
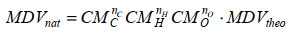
(8) |
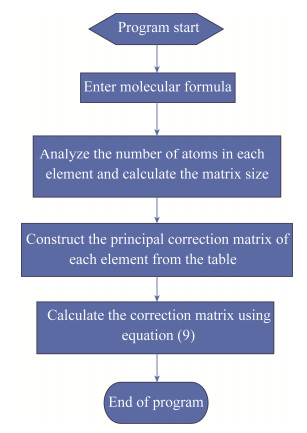
以上算法在Python平台中进行了代码实现，代码上传至开源软件库Gitee中(https://gitee.com/bioexplore/py-iso-correction)。软件编写的流程图如图 2所示。
|
| 图 2 计算给定分子式的天然同位素修正矩阵算法的流程图 Fig. 2 Flow diagram of the algorithm for calculating the natural isotope correction matrix for a given molecular formula. |
| |
首先定义了几个在后期计算中将会用到的函数，先在Python环境下运行该程序，然后在命令行中输入如表 2所示的第1行代码，还是以葡萄糖(C6H12O6) 为例，运行后就得到了葡萄糖分子的矫正矩阵的逆矩阵crr_matrix，然后再将质谱得到的MDVnat数据依次输入，如第2行代码，假设质谱最小只能得到M+7的数据，注意向量MDVnat的行数需要与矫正矩阵一致，质谱无法检测或数值太小的数据用0补齐。最后输入第3行代码，实现逆矩阵和向量MDVnat相乘得到矫正后的向量MDVtheo，corrected_mdv。
表 2 tools.py运行后需输入的命令行
Table 2 Command lines to be entered after running tools.py
| No. | Command line |
| 1 | crr_matrix=get_corr_matrix_of_molecule(“C6H12O6”) |
| 2 | mdv_mol=[M+0, M+1, M+2, M+3, M+4, M+5, M+6, M+7, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] |
| 3 | corrected_mdv=np.dot(crr_matrix, mdv_mol) |
质谱级葡萄糖(Sigma Aldrich) U-12C (99%)、1-13C (98%)和U-13C (98%)。
2.2 样品准备本文采用的菌株是A. niger B36[21-22]。首先将在–80 ℃保藏的A. niger B36孢子液涂布于含有完全培养基的平板中，培养4−5 d，用以富集孢子。之后每个平板用5−8 mL生理盐水将孢子洗脱，汇集后使孢子液的浓度达到107–108个孢子/mL。发酵培养基成分如表 3所示。采用500 mL发酵罐，装液量350 mL，以109个孢子/L的接种量将孢子液注入发酵罐中，然后在罐内不通气的情况下以250 r/min的转速培养3 h，让孢子萌发。3 h后通气量500 mL/min，转速升为750 r/min，进入批发酵阶段，同时以2 mol/L NaOH维持培养基的pH 3。12–18 h后通过观察菌体的发酵曲线图发现菌体开始进入指数生长后期时开始补料，补料速率为0.08 L/h，补料培养基成分如表 4所示。观察生长曲线图发现，菌体生长稳定后切换补料培养基，改为带有同位素标记的葡萄糖，成分见表 4。在补料5个发酵体积后可认为发酵进入恒化稳态，此时快速取样[23]检测A. niger B36的胞内代谢物同位素标记分布。
表 3 上述提及的培养基组成
Table 3 The composition of media used in this study
| Name | Concentration |
| Complete medium | |
| Yeast extract Casamino acid 50% C6H12O6 50* Asp+Na* 1 mol/L MgSO4 Trace elementb* Agar |
5 g/L 1 g/L 1 mL/L 1 mL/L 200 μL/L 100 μL/L 1.5% (W/W) |
| Batch fermentation medium | |
| C6H12O6·H2O NH4Cl KH2PO4 KCl MgSO4·7H2O Trace elementb* Antifoam Yeast extract |
9.9 g/L 4.5 g/L 1.5 g/L 0.5 g/L 0.5 g/L 1 mL/L 1 mL/L 0.03 g/L |
| a*: components include: 297.5 g/L NaNO3, 26.1 g/L KCl, 74.8 g/L KH2PO4, pH 5.5.b*: components include: 10 g/L EDTA, 0.32 g/L CoCl2·6H2O, 4.40 g/L ZnSO4·7H2O, 0.315 g/L CuSO4·5H2O, 1.01 g/L MnCl2·4H2O, 0.22 g/L (NH4)6 Mn7O24·4H2O, 1.11 g/L CaCl2, 1.00 g/L FeSO4·7H2O, pH 4.0. | |
表 4 补料培养基组成
Table 4 The composition of feed media
| Name | Concentration |
| Feed medium | |
| C6H12O6·H2O | 8.5 g/L |
| NH4Cl | 4.5 g/L |
| KH2PO4 | 1.5 g/L |
| KCl | 0.5 g/L |
| MgSO4·7H2O | 0.5 g/L |
| Trace elementb* | 1.0 mL/L |
| Antifoam | 1.0 mL/L |
| Feed media with isotopes | |
| C6H12O6 | 8.5 g/L c* |
| NH4Cl | 4.5 g/L |
| KH2PO4 | 1.5 g/L |
| KCl | 0.5 g/L |
| MgSO4·7H2O | 0.5 g/L |
| Trace elementb* | 1.0 mL/L |
| Antifoam | 1.0 mL/L |
| c*: components include: 50% (W/W) U-12C C6H12O6, 20% (W/W) 1-13C C6H12O6, 30% (W/W) U-13C C6H12O6. | |
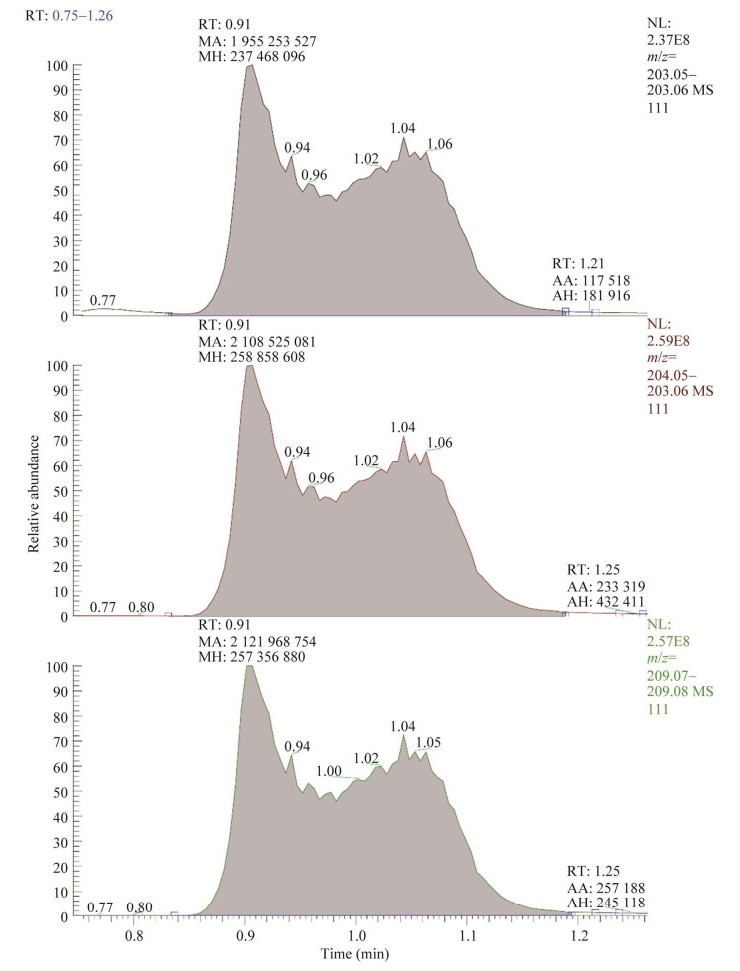
将上述方法应用于标准葡萄糖的测定以验证修正算法的正确性。首先，取质谱级葡萄糖U-12C、1-13C、U-13C各1 mmol/L，等体积混合后进质谱，各同位素峰图如图 3所示，取相应质量分子数的峰面积之比，归一化后作为MDVnat输入。按照表 5代码依次输入后执行修正程序，表 5的第2条代码中的mdv_mol即为MDVnat。最后输入第4行代码并执行，得到的结果如表 5中的第5行代码所示。为了更加直观地得到结果，MDVnat的输入中仅有M0、M1和M6有数值，其余MID均为0，这就导致在矩阵运算结果中出现负值。
|
| 图 3 3种C同位素标记葡萄糖混标的GC-MS结果 Fig. 3 GC-MS results for mixed labels of standard glucose. 从上往下依次为M0、M1和M6的出峰情况 From top to bottom, the peaks are M0, M1 and M6 in order. |
| |
表 5 混标葡萄糖同位素分布修正时需输入的命令行
Table 5 Command lines to be entered for the correction of isotope distribution of mixed glucose standards
| No. | Command line |
| 1 | crr_matrix=get_corr_matrix_of_molecule (“C6H12O6”) |
| 2 | mdv_mol=[0.315 984, 0.344 448, 0, 0, 0, 0, 0.339 568, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] |
| 3 | corrected_mdv = np.dot(crr_matrix, mdv_mol) |
| 4 | corrected_mdv |
| 5 | array([3.432 502 50e-01, 3.498 582 63e-01, -2.974 424 45e-02, -3.263 157 34e-03, 3.142 444 05e-04, 1.878 653 18e-05, 3.688 672 45e-01, -2.612 680 81e-02, -3.484 014 28e-03, 2.911 594 06e-04, 2.031 168 89e-05, -1.952 732 19e-06, -9.326 648 78e-08, 1.016 115 36e-08, 3.692 009 21e-10, -4.513 839 51e-11, -1.318 156 64e-12, 1.796 774 90e-13, 4.357 201 36e-15, -6.594 257 35e-16, -1.355 791 77e-17, 2.272 733 39e-18, 4.015 739 93e-20, -7.449 519 50e-21, -1.141 038 91e-22, 2.343 439 85e-23, 3.127 483 57e-25, -7.123 112 50e-26, -8.301 374 61e-28, 2.102 980 57e-28, 2.139 597 65e-30]) |
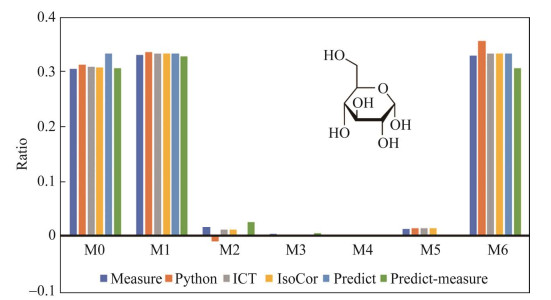
为了评估Python修正程序的有效性，用带有不同13C标记的葡萄糖标准品配制混合溶液，物质的量浓度比例为12C︰1-13C︰U-13C=1︰1︰1，样品通过LC-MS/MS进行分析。图 4包含了每种同位素MID的理论值(predict)、理论测量值(通过理论值反向执行程序得出，predict-measure)、测量值(measure) 以及3种软件对该测量值的修正结果(本工作(Python), ICT, IsoCor)。从图 4的Python、ICT、IsoCor的修正结果可以看出，这3种工具的修正结果具有一致性。
关于混合溶液的组成所预期的测量值predict- measure，当把测得的未修正数据即实际测量值与预期的未修正数据进行比较时，图 4显示了实际测量值在M+0、M+1处与预期测量值误差范围在0.1%以内，而M+6处与预期测量值差距在7%以内，且两者间的偏差与理论值和3种修正程序得出的结果之间的偏差具有相同的趋势，这表明3种修正程序得出的结果具有相同的可信度。Predict- measure和measure之间出现差异的原因很可能是测量或峰值整合不准确。理论和实际的测量值之间的偏差可能或大或小，若与1个小得多的理论测量值相比，理论和实际的测量值之间则会出现较大的差异，这体现了同位素示踪剂纯度与不准确测量相结合的效果(这在低动态范围内可能特别明显)。对于比例丰度较低的同位素，在未修正数据中偏差的相对大小在修正后会大幅增加。
|
| 图 4 用已知组成的葡萄糖标品混合物对修正软件进行对比分析 Fig. 4 Assessment of the calibration software with a mixture of glucose specimens of known composition. x轴的M0–M6对应于7种带有不同中子数量的葡萄糖同位素，分组条形图描述了测量值(measure)、理论值(predict)、理论测量值(predict-measure) 以及3种修正方法获得的结果(Python, ICT, IsoCor) 之间的比较 M0–M6 on the x-axis corresponds to seven glucose isotopes with different neutron numbers, and the grouped bars depict the measured (measure), theoretical (predict), and theoretical measured (predict-measure) values, as well as the results obtained by the three calibration methods (Python, ICT, IsoCor) are compared with each other. |
| |
针对鲁洪中论文里的代谢流计算软件INCA对A. niger中心碳代谢流模拟计算开展验证[24]。由于其在计算代谢流时未进行天然同位素的修正，因此本节将在其数据基础上，运用不同的修正方法，对其A. niger CBS513.88菌株数据修正后再进行代谢流计算，数据修正结果如表 6所示，并将不同修正方法计算所得到的代谢物同位素分布数据，输入同一计算模型中，得到不同的代谢通量图，比较结果如图 5所示。
表 6 用IsoCor、ICT以及Python对鲁洪中论文数据[24]进行修正的结果
Table 6 Correction of the data in Lu Hongzhong's paper by IsoCor, ICT, and Python
| Amino acid fragment | MDV | Corrected results | |||
| Measured | IsoCor | ICT | Python | ||
| Ala85 | M+0 | 0.669 0 | 0.687 0 | 0.672 6 | 0.688 8 |
| M+1 | 0.165 0 | 0.150 0 | 0.162 6 | 0.151 1 | |
| M+2 | 0.166 0 | 0.163 0 | 0.164 7 | 0.165 2 | |
| Ala57 | M+0 | 0.631 0 | 0.657 0 | 0.636 0 | 0.658 6 |
| M+1 | 0.185 0 | 0.166 0 | 0.183 1 | 0.167 5 | |
| M+2 | 0.047 0 | 0.040 0 | 0.043 8 | 0.039 5 | |
| M+3 | 0.137 0 | 0.137 0 | 0.137 1 | 0.140 6 | |
| Asp85 | M+0 | 0.505 5 | 0.527 5 | 0.510 7 | 0.528 9 |
| M+1 | 0.300 3 | 0.290 1 | 0.300 5 | 0.293 4 | |
| M+2 | 0.137 1 | 0.128 7 | 0.133 7 | 0.128 4 | |
| M+3 | 0.057 1 | 0.053 7 | 0.055 1 | 0.052 6 | |
| Asp57 | M+0 | 0.449 0 | 0.475 0 | 0.454 8 | 0.476 8 |
| M+1 | 0.295 0 | 0.286 0 | 0.296 1 | 0.287 4 | |
| M+2 | 0.127 0 | 0.116 0 | 0.123 1 | 0.115 8 | |
| M+3 | 0.094 0 | 0.090 0 | 0.092 0 | 0.091 3 | |
| M+4 | 0.035 0 | 0.033 0 | 0.033 9 | 0.031 3 | |
| Glu85 | M+0 | 0.412 0 | 0.435 0 | 0.416 7 | 0.436 0 |
| M+1 | 0.285 0 | 0.276 0 | 0.285 8 | 0.279 5 | |
| M+2 | 0.222 0 | 0.216 0 | 0.220 3 | 0.217 6 | |
| M+3 | 0.062 0 | 0.056 0 | 0.059 6 | 0.052 4 | |
| M+4 | 0.019 0 | 0.017 0 | 0.017 5 | 0.015 8 | |
| Glu57 | M+0 | 0.346 7 | 0.371 0 | 0.351 6 | 0.371 9 |
| M+1 | 0.285 7 | 0.280 0 | 0.287 5 | 0.283 3 | |
| M+2 | 0.218 8 | 0.212 0 | 0.217 2 | 0.213 4 | |
| M+3 | 0.106 9 | 0.100 0 | 0.104 7 | 0.098 4 | |
| M+4 | 0.031 0 | 0.027 0 | 0.029 0 | 0.024 9 | |
| M+5 | 0.011 0 | 0.010 0 | 0.010 1 | 0.009 2 | |
| Ser85 | M+0 | 0.653 0 | 0.672 0 | 0.658 0 | 0.673 8 |
| M+1 | 0.286 0 | 0.274 0 | 0.284 7 | 0.276 6 | |
| M+2 | 0.061 0 | 0.054 0 | 0.057 3 | 0.052 4 | |
| Ser57 | M+0 | 0.591 0 | 0.617 0 | 0.597 3 | 0.618 3 |
| M+1 | 0.264 0 | 0.249 0 | 0.263 5 | 0.252 0 | |
| M+2 | 0.104 0 | 0.096 0 | 0.100 0 | 0.094 8 | |
| M+3 | 0.041 0 | 0.038 0 | 0.039 2 | 0.037 3 | |
| Thr85 | M+0 | 0.529 0 | 0.551 0 | 0.533 5 | 0.552 2 |
| M+1 | 0.275 0 | 0.263 0 | 0.274 4 | 0.265 5 | |
| M+2 | 0.136 0 | 0.129 0 | 0.133 5 | 0.129 0 | |
| M+3 | 0.060 0 | 0.057 0 | 0.058 6 | 0.056 3 | |
| Thr57 | M+0 | 0.486 0 | 0.513 0 | 0.491 4 | 0.514 3 |
| M+1 | 0.269 0 | 0.256 0 | 0.269 1 | 0.258 6 | |
| M+2 | 0.120 0 | 0.111 0 | 0.116 7 | 0.110 2 | |
| M+3 | 0.094 0 | 0.091 0 | 0.092 7 | 0.091 9 | |
| M+4 | 0.031 0 | 0.029 0 | 0.030 1 | 0.027 3 | |
| Val57 | M+0 | 0.502 5 | 0.535 0 | 0.507 3 | 0.536 5 |
| M+1 | 0.206 2 | 0.186 0 | 0.205 3 | 0.187 1 | |
| M+2 | 0.134 1 | 0.128 0 | 0.132 1 | 0.128 6 | |
| M+3 | 0.113 1 | 0.111 0 | 0.112 6 | 0.111 6 | |
| M+4 | 0.023 0 | 0.020 0 | 0.022 0 | 0.016 9 | |
| M+5 | 0.021 0 | 0.020 0 | 0.020 6 | 0.020 7 | |
| Val85 | M+0 | 0.511 5 | 0.538 0 | 0.515 2 | 0.538 8 |
| M+1 | 0.205 2 | 0.187 0 | 0.203 9 | 0.189 1 | |
| M+2 | 0.218 2 | 0.216 0 | 0.217 6 | 0.218 7 | |
| M+3 | 0.051 1 | 0.046 0 | 0.049 9 | 0.042 2 | |
| M+4 | 0.014 0 | 0.013 0 | 0.013 4 | 0.011 9 | |
|
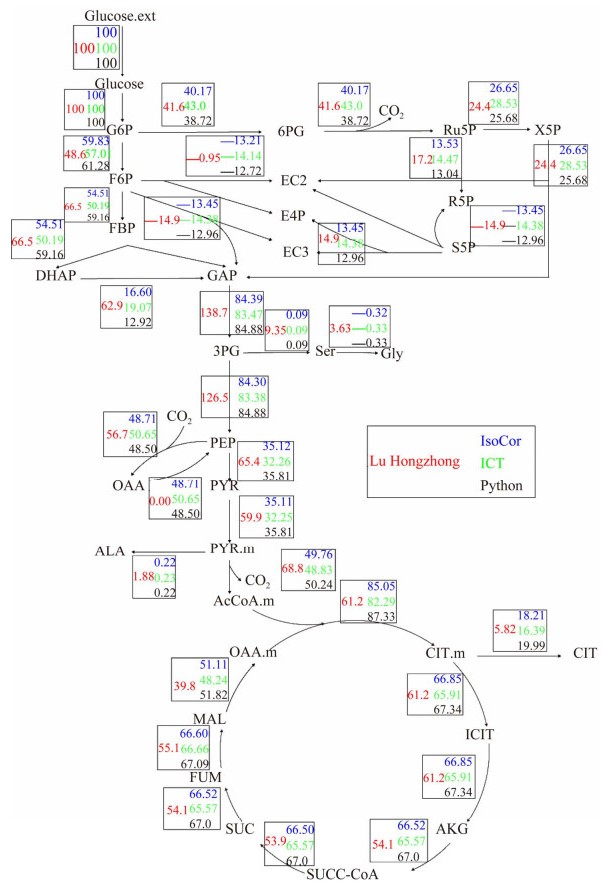
| 图 5 使用3种修正方法后INCA计算的代谢流结果 Fig. 5 Metabolic flow calculated by INCA after correction with the three methods. 红色数据为鲁洪中未修正的代谢流结果[24]，蓝色数据为IsoCor修正的代谢流结果，绿色数据为ICT修正的代谢流结果，黑色数据为Python修正的代谢流结果 Red data are the uncorrected metabolic flow results in Lu Hongzhong, blue data are the corrected metabolic flow result by IsoCor, green data are the corrected metabolic flow result by ICT, black data are the corrected metabolic flow result by Python. |
| |
从表 6可以看出，在经过不同软件的修正后，原始数据均有不同程度的偏离，从整体上来看，IsoCor的修正结果与Python的结果接近，而ICT的修正结果与文献测量值相差不大。将这些修正后的数据输入INCA，利用与文献相同的模型进行计算后，得出的胞内代谢网络通量也有所区别。如图 5所示，在分支节点处，这3种软件所得结果相差较大，例如反应6-磷酸果糖(fructose-6-phosphate, F6P)↔1, 6-二磷酸果糖(fructose-1, 6-bisphosphate, FBP)，IsoCor的计算通量为54.51%，ICT的计算通量为50.19%，而Python的计算通量为59.16%，但是在一些通量较小的反应中，三者之间没有明显区别，如反应3-磷酸甘油酸(3-phosphoglycerate, 3PG)→丝氨酸(serine, Ser)，这可能是由于3种软件的算法逻辑不同导致的[25]。
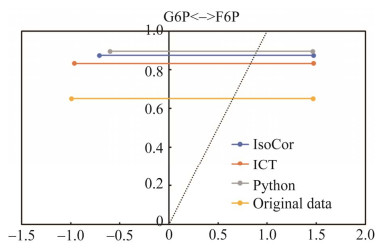
图 6所示为鲁洪中模型的其中一步反应，使用3种修正方法后INCA计算的代谢流置信区间与原文数据的比对。由图中可以看出，测量数据在经过修正计算后，均能得到相差不大的95%置信区间上限，且相应代谢通量的95%置信区间范围均比原始数据的区间范围小，其中区间范围最小的是Python修正后的结果，即本研究所构建的修正方法。
|
| 图 6 使用3种修正方法后INCA计算的可逆反应G6P↔F6P通量置信区间与原文数据的比对 Fig. 6 Confidence intervals of INCA-calculated reversible reaction G6P↔F6P fluxes after correction with the three methods compared to the original data. 图中虚线与实线相交的点为对应方法下INCA计算的代谢通量值 The points where the dashed and solid lines intersect are the INCA-calculated metabolic flux values under the corresponding methods. |
| |
检测的结果如表 7所示，其中有4种氨基酸分子的子离子数据，作为小分子，氨基酸的天然同位素校正原理与其他小分子代谢物一样。将测得的数据输入本文构建的修正方法得到修正后的实验数据，分别将原始数据和修正后的实验数据输入代谢流计算模型中，得到如表 7所示的胞内代谢物同位素分布模拟值，通过比较修正前后的测量值，发现所有测得的代谢物MDV中只有M0在修正后有所增加，其余M1和M2等MID均减少，造成如此计算结果的原因是自然界中不带同位素标记的原子占比90%以上。
表 7 同位素代谢稳定状态下细胞内氨基酸代谢物片段的MDV与本文程序模拟的氨基酸片段MDV比较
Table 7 MDV of intracellular amino acid metabolites in the steady state of isotope metabolism versus the MDV of amino acid metabolites simulated by the procedure in this study
| Metabolite | MDV | 0.1 h–1 | |||
| Measured | Corrected | Simulated without correct d* | Simulated after correct e* | ||
| MAL | M0 | 0.332 4 | 0.352 0 | 0.282 4 | 0.295 2 |
| M1 | 0.266 8 | 0.265 9 | 0.287 8 | 0.286 3 | |
| M2 | 0.209 4 | 0.205 3 | 0.276 6 | 0.272 6 | |
| M3 | 0.139 7 | 0.135 1 | 0.113 4 | 0.108 0 | |
| M4 | 0.051 7 | 0.045 9 | 0.040 0 | 0.037 9 | |
| Ala-57 | M0 | 0.485 9 | 0.507 1 | 0.619 8 | 0.630 6 |
| M1 | 0.192 7 | 0.181 4 | 0.077 2 | 0.067 2 | |
| M2 | 0.102 4 | 0.097 5 | 0.024 1 | 0.023 3 | |
| M3 | 0.219 0 | 0.223 8 | 0.278 8 | 0.278 8 | |
| Val-57 | M0 | 0.299 2 | 0.319 4 | 0.399 9 | 0.413 8 |
| M1 | 0.184 1 | 0.176 8 | 0.084 1 | 0.072 4 | |
| M2 | 0.174 6 | 0.173 6 | 0.205 5 | 0.206 8 | |
| M3 | 0.186 4 | 0.187 2 | 0.204 4 | 0.204 1 | |
| M4 | 0.080 0 | 0.072 8 | 0.022 6 | 0.019 5 | |
| M5 | 0.075 7 | 0.075 2 | 0.083 5 | 0.083 3 | |
| Ser-57 | M0 | 0.432 6 | 0.452 6 | 0.619 8 | 0.630 6 |
| M1 | 0.231 9 | 0.224 9 | 0.077 2 | 0.067 2 | |
| M2 | 0.144 4 | 0.139 1 | 0.024 1 | 0.023 3 | |
| M3 | 0.191 1 | 0.192 9 | 0.278 8 | 0.278 8 | |
| Glu-57 | M0 | 0.176 0 | 0.188 8 | 0.212 2 | 0.223 7 |
| M1 | 0.203 9 | 0.207 0 | 0.258 6 | 0.259 8 | |
| M2 | 0.251 8 | 0.255 3 | 0.278 5 | 0.276 3 | |
| M3 | 0.197 0 | 0.193 3 | 0.164 6 | 0.158 6 | |
| M4 | 0.113 2 | 0.106 8 | 0.067 8 | 0.064 4 | |
| M5 | 0.058 0 | 0.053 5 | 0.018 3 | 0.017 1 | |
| d*: denotes the result obtained by substituting uncorrected raw data into the metabolic flow computational model, and e*: denotes the result obtained by substituting Python corrected raw data into the computational model. | |||||
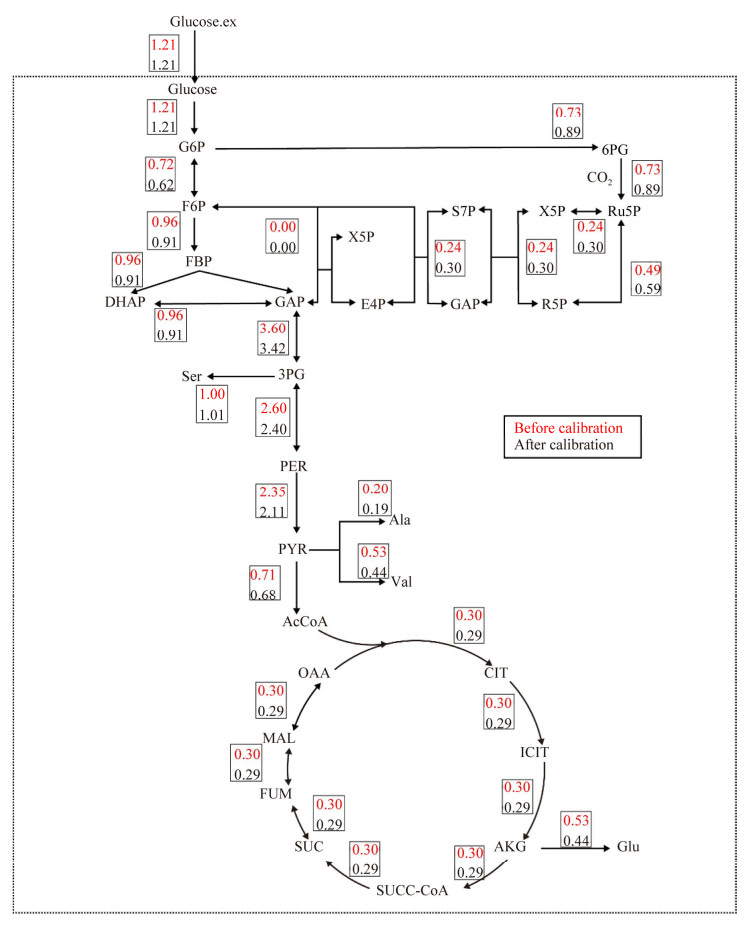
将两者同时输入A. niger代谢流分析模型，得到结果如图 7所示的胞内代谢通量分布图。由图 7可以看出，矫正前后对代谢流分析结果影响较大。6-磷酸葡萄糖(glucose-6-phosphate, G6P) 作为糖酵解(Embden-Meyerhof-Parnas, EMP) 途径和磷酸戊糖途径(pentose phosphate pathway, PPP) 的分支点，修正后流入EMP途径的流量值更小，同时流入PPP途径的碳流量值较大。
|
| 图 7 Aspergillus niger B36胞内代谢物同位素丰度修正前后的模拟计算代谢通量对比 Fig. 7 Comparison of calculated metabolic fluxes of metabolites in Aspergillus niger B36 before and after correction of isotopic abundance. 红色数据代表修正前，黑色数据代表修正后 The red data represents before calibration and the black data represents after calibration. |
| |
对于三羧酸循环(tricarboxylic acid cycle, TCA) 来说，特别是其中的柠檬酸(citric acid, CIT)，由于修正后流入EMP途径的碳流量减少，导致TCA循环通量也有所下降。在实验条件保持不变的情况下，仅对代谢物同位素丰度分布进行修正，胞内代谢通量分布发生了较明显的改变，说明了天然同位素修正对代谢流分析具有重要作用。
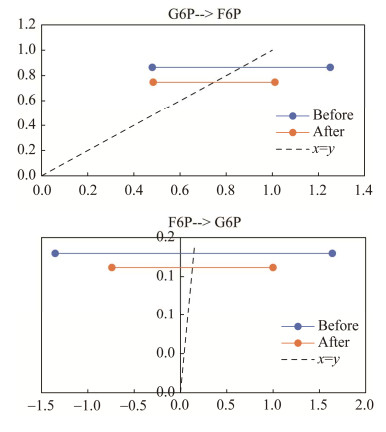
A. niger计算模型结果是由代码确定代谢网络中一部分的自由通量，从而确定整个网络的通量分布。本研究利用A. niger代谢网络中的一个自由通量，对修正前后胞内通量95%置信区间的变化进行分析，如图 8所示，在反应G6P↔F6P中，相较于MDV未修正得到代谢通量模拟值的置信区间，其正向反应和逆向反应在MDV修正后所得的置信区间范围均更小，同时两者所得到的最优解也相差无几，这说明本研究的修正方法让MFA的计算结果更加具有可信度。
|
| 图 8 可逆反应G6P↔F6P的正向反应和逆向反应通量置信区间修正前后对比 Fig. 8 Comparison of the confidence intervals of forward and reverse reaction fluxes before and after correction for the reversible reaction G6P↔F6P. 图中虚线与水平线的交点即为相应情况下的最优通量解 The intersection of the dashed and horizontal lines in the figure is the optimal flux solution for the corresponding case. |
| |
本文针对天然稳定性同位素分布对于质谱检测同位素丰度分布数据的影响，提出了一种用Python语言构建的修正方法，该方法以一种新的角度构建修正矩阵，解决了修正过程中计算繁杂的缺点。本文构建的方法考虑到了某一分子中所有可能出现的同位素异构体，随着检测仪器精度的提高，使用该方法修正的质谱测量值越接近真实值，能够为代谢流计算提供更加具有可信度的数据，给后续13C代谢流分析软件构建打下良好的算法及数据基础。
参考文献
| [1] |
Wiechert W. 13C metabolic flux analysis. Metab Eng, 2001, 3(3): 195-206. DOI:10.1006/mben.2001.0187
|
| [2] |
Antoniewicz MR. Methods and advances in metabolic flux analysis: a mini-review. J Ind Microbiol Biotechnol, 2015, 42(3): 317-325. DOI:10.1007/s10295-015-1585-x
|
| [3] |
Dai ZW, Locasale JW. Understanding metabolism with flux analysis: from theory to application. Metab Eng, 2017, 43(Pt B): 94-102.
|
| [4] |
Antoniewicz MR. 13C metabolic flux analysis: optimal design of isotopic labeling experiments. Curr Opin Biotechnol, 2013, 24(6): 1116-1121. DOI:10.1016/j.copbio.2013.02.003
|
| [5] |
Niedenführ S, Wiechert W, Nöh K. How to measure metabolic fluxes: a taxonomic guide for 13C fluxomics. Curr Opin Biotechnol, 2015, 34: 82-90. DOI:10.1016/j.copbio.2014.12.003
|
| [6] |
Wiechert W, Nöh K. Isotopically non-stationary metabolic flux analysis: complex yet highly informative. Curr Opin Biotechnol, 2013, 24(6): 979-986. DOI:10.1016/j.copbio.2013.03.024
|
| [7] |
Crown SB, Antoniewicz MR. Publishing 13C metabolic flux analysis studies: a review and future perspectives. Metab Eng, 2013, 20: 42-48. DOI:10.1016/j.ymben.2013.08.005
|
| [8] |
Yasemi M, Jolicoeur M. Modelling cell metabolism: a review on constraint-based steady-state and kinetic approaches. Processes, 2021, 9(2): 322. DOI:10.3390/pr9020322
|
| [9] |
Buescher JM, Antoniewicz MR, Boros LG, et al. A roadmap for interpreting 13C metabolite labeling patterns from cells. Curr Opin Biotechnol, 2015, 34: 189-201. DOI:10.1016/j.copbio.2015.02.003
|
| [10] |
Dalman T, Wiechert W, Nöh K. A scientific workflow framework for 13C metabolic flux analysis. J Biotechnol, 2016, 232: 12-24. DOI:10.1016/j.jbiotec.2015.12.032
|
| [11] |
Moseley HN. Correcting for the effects of natural abundance in stable isotope resolved metabolomics experiments involving ultra-high resolution mass spectrometry. BMC Bioinformatics, 2010, 11: 139. DOI:10.1186/1471-2105-11-139
|
| [12] |
Jungreuthmayer C, Neubauer S, Mairinger T, et al. ICT: isotope correction toolbox. Bioinformatics, 2016, 32(1): 154-156.
|
| [13] |
Millard P, Letisse F, Sokol S, et al. IsoCor: correcting MS data in isotope labeling experiments. Bioinformatics, 2012, 28(9): 1294-1296. DOI:10.1093/bioinformatics/bts127
|
| [14] |
Rosenblatt J, Chinkes D, Wolfe M, et al. Stable isotope tracer analysis by GC-MS, including quantification of isotopomer effects. Am J Physiol, 1992, 263(3 Pt 1): E584-E596.
|
| [15] |
Midani FS, Wynn ML, Schnell S. The importance of accurately correcting for the natural abundance of stable isotopes. Anal Biochem, 2017, 520: 27-43. DOI:10.1016/j.ab.2016.12.011
|
| [16] |
Niedenführ S, Ten Pierick A, Dam PTV, et al. Natural isotope correction of MS/MS measurements for metabolomics and 13C fluxomics. Biotechnol Bioeng, 2016, 113(5): 1137-1147. DOI:10.1002/bit.25859
|
| [17] |
Wang YJ, Parsons LR, Su XY. AccuCor2: isotope natural abundance correction for dual-isotope tracer experiments. Lab Invest, 2021, 101(10): 1403-1410. DOI:10.1038/s41374-021-00631-4
|
| [18] |
Millard P, Letisse F, Sokol S, et al. Correction of MS data for naturally occurring isotopes in isotope labelling experiments. Methods Mol Biol, 2014, 1191, 197-207.
|
| [19] |
Van Winden WA, Wittmann C, Heinzle E, et al. Correcting mass isotopomer distributions for naturally occurring isotopes. Biotechnol Bioeng, 2002, 80(4): 477-479. DOI:10.1002/bit.10393
|
| [20] |
Nilsson R. Validity of natural isotope abundance correction for metabolic flux analysis. Math Biosci, 2020, 330: 108481. DOI:10.1016/j.mbs.2020.108481
|
| [21] |
Kwon MJ, Jørgensen TR, Nitsche BM, et al. The transcriptomic fingerprint of glucoamylase over-expression in Aspergillus niger. BMC Genomics, 2012, 13: 701.
|
| [22] |
Sui YF, Schütze T, Ouyang LM, et al. Engineering cofactor metabolism for improved protein and glucoamylase production in Aspergillus niger. Microb Cell Fact, 2020, 19(1): 198.
|
| [23] |
王帅. 产糖化酶菌株黑曲霉在底物和溶解氧浓度波动下的胞内代谢物浓度动态响应规律探究[D]. 上海: 华东理工大学, 2019. Wang S. Intracellular dynamic response of glycosylase high yield Aspergillus niger under the concentration gradient of substrates and dissolved oxygen[D]. Shanghai: East China University of Science and Technology, 2019 (in Chinese). |
| [24] |
鲁洪中. 基于13C代谢流和基因组规模代谢网络模型的黑曲霉产糖化酶代谢调控机理研究[D]. 上海: 华东理工大学, 2016. Lu HZ. Investigation of metabolic regulation mechanism in enzyme production by Aspergillus niger based on 13C metabolic flux and genome scale metabolic network model[D]. Shanghai: East China University of Science and Technology, 2016 (in Chinese). |
| [25] |
Mairinger T, Wegscheider W, Peña DA, et al. Comprehensive assessment of measurement uncertainty in 13C-based metabolic flux experiments. Anal Bioanal Chem, 2018, 410(14): 3337-3348.
|